阅读材料:
例:说明代数式 x2+1 + (x-3)2+4 的几何意义,并求它的最小值.
解: x2+1 + (x-3)2+4 =" (x-0)2+12" + (x-3)2+22 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 (x-0)2+12 可以看成点P与点A(0,1)的距离, (x-3)2+22 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B="3" 2 ,即原式的最小值为3 2 .
根据以上阅读材料,解答下列问题:
(1)代数式 (x-1)2+1 + (x-2)2+9 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B (2,3)的距离之和.(填写点B的坐标)
(2)代数式 x2+49 + x2-12x+37 的最小值为.
如图,每个小方格都是边长为1个单位
的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF ∽△ABC,且相似比为2∶1;
(2)求△ABC中AC边上的高;
(3)若△ABC外接圆的圆心为P,则点P的坐标为
先化简,再计算: ,其中
,其中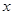 是方程
是方程 的正数根.
的正数根.
解下列方程
(1)
(2)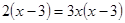
(3)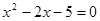 (配方法)
(配方法)
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
求证:(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ,求⊙O的半径。
,求⊙O的半径。
在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出( 在
在 轴上),运动员孙可在距
轴上),运动员孙可在距 点6米的
点6米的 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点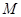 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取 )
)
(3)孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点 再向前跑多少米?(取
再向前跑多少米?(取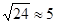 )
)