已知：一次函数y=3x－2的图象与某反比例函数的图象的一个公共点的横坐标为1．
（1）(3分)求该反比例函数的解析式；
（2）(3分)将一次函数y=3x－2的图象向上平移4个单位，求平移后的图象与反比例函数图象的交点坐标；
（3）(2分)请直接写出一个同时满足如下条件的函数解析式：
①函数的图象能由一次函数y=3x－2的图象绕点（0，－2）旋转一定角度得到；
②函数的图象与反比例函数的图象没有公共点．
动手实验：利用矩形纸片（图1）剪出一个正六边形纸片；利用这个正六边形纸片做一个如图（2）无盖的正六棱柱（棱柱底面为正六边形）；
（1）做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少？
（2）在（1）的前提下，当矩形的长为2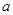
时，要使无盖正六棱柱侧面积最大，正六棱柱的高为多少？并求此时矩形纸片的利用率？（矩形纸片的利用率=
无盖正六棱柱的表面积/矩形纸片的面积）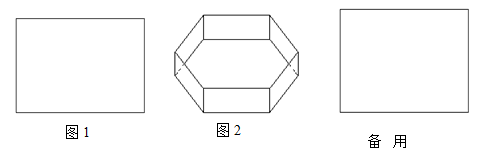
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需7200元．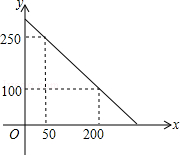
（1）根据图象，求y与x之间的函数关系式；
（2）求甲、乙两种品牌的文具盒进货单价；
（3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？
已知：如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．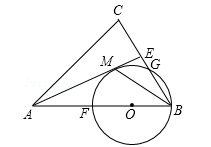
（1）求证：AE与⊙O相切；
（2）当BC=4，cosC=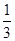
时，求⊙O的半径．
如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BFQ＝60°，EF＝1km．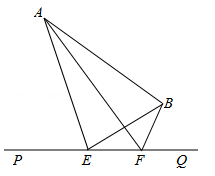
（1）判断线段AB与AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）．
甲、乙两商场同时开业，为了吸引顾客，都举办有奖酬宾活动，凡购物满100元，均可得到一次摸奖的机会．在一个纸盒里装有2个红球和2个白球，除颜色外，其他全部相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券的多少（如下表）．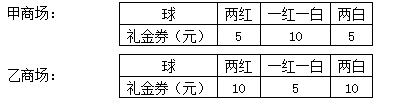
（1）请你用列表法（或画树状图）求出摸到一红一白的概率；
（2）如果只考虑中奖因素，你将会选择去哪个商场购物？请说明理由．