定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____,
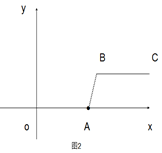
当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______
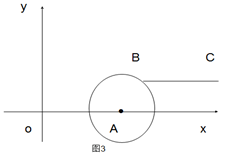
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似,若存在,求出m的值;若不存在,请说明理由.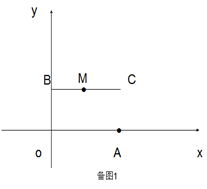
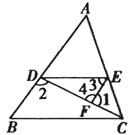
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,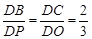 .
.
(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的值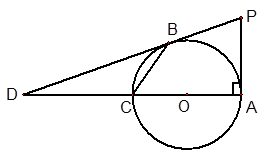
若三角形三条边的长度依次为 ,
,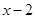 ,
, ,则
,则 的取值范围是多少?
的取值范围是多少?
三条公路两两相交,现想建一加油站,若想到三条公路的距离相等,应如何建该加油站?
已知二次函数:(1)y=x2+x-2 (2)y=x2-6x+9 (3)y=x2-x+1的图象如图所示,观察图象解决下列问题:
(1)以上二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?
(2)当x取公共点的横坐标时,二次函数的值是多少?由此,你能直接写出相应的一元二次方程的根吗?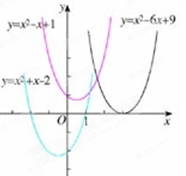
如图,已知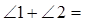 180°,
180°, ,试说明
,试说明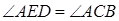 .
.