设随机变量X服从N(0,1),记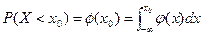 .已知
.已知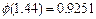 ,求下列各式的值:
,求下列各式的值:
(1)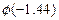 ;(2)P(|X|<1.44).
;(2)P(|X|<1.44).
某人骑自行车上班,第一条路线较短但拥挤,到达时间X(分钟)服从正态分布N(5,1);第二条路较长不拥挤,X服从N(6,0.16).有一天她出发时离点名时间还有7分钟,问他应选哪一条路线?若离点名时间还有6.5分钟,问他应选哪一条路线?
如果某地成年男子的身高X~N(175,62)(单位:cm),该地公共汽车门的高度设计为2米,则该地成年男子与车门顶部碰头的概率是否在1%以下?
某正态曲线的密度函数是偶函数,而且该函数的最大值为 ,求总体位于区间[-4,-2]的概率.
,求总体位于区间[-4,-2]的概率.
某厂生产的圆柱形零件的外径ε~N(4,0.25).质检人员从该厂生产的1000件零件中随机抽查一件,测得它的外径为5.7cm.试问该厂生产的这批零件是否合格?