产自庆元县百山祖山麓一带的“沁园春”茶叶是丽水市知名品牌．现该品牌旗下一茶厂有采茶工人30人，每人每天采鲜茶叶“炒青”20千克或鲜茶叶“毛尖”5千克.已知生产每千克成品茶叶所需鲜茶叶和销售每千克成品茶叶所获利润如下表：
| 类别 |
生产1千克成品茶叶所需鲜茶叶（千克） |
销售1千克成品茶叶所获利润（元） |
| 炒青 |
4 |
40 |
| 毛尖 |
5 |
120 |
（1）若安排x人采“炒青”，则可采鲜茶叶“炒青” 千克，采鲜茶叶“毛尖” 千克．
（2）若某天该茶厂工生产出成品茶叶102千克，则安排采鲜茶叶“炒青”与“毛尖”各几人？
（3）根据市场销售行情，该茶厂的生产能力是每天生产成品茶叶不少于100千克且不超过110千克，如果每天生产的茶叶全部销售，如何分配采茶工人能使获利最大？最大利润是多少？
先化简
，再从−2，0，1，2中选择一个合适的数代入，求出这个代数式的值．
解方程组：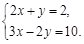
计算：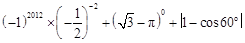
．
如图，正方形ABCD的顶点A、B分别在y轴和x轴上，且A点的坐标为（0,1），正方形的边长为
.
(1) 直接写出D、C两点的坐标；
（2）求经过A、D、C三点的抛物线的关系式；
（3）若正方形以每秒
个单位长度的速度匀速沿射线
下滑，直至顶点
落在
轴上时停止．设正方形落在轴下方部分的面积为S，求S关于滑行时间
的函数关系式，并写出相应自变量的取值范围；
（4）在（3）的条件下，抛物线与正方形一起平移，到顶点落在轴上时，求抛物线上
两点间的抛物线弧所扫过的面积．
△ABC是一块等边三角形的废铁片，利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F、G分别落在AC、AB上．
(1) 证明：△BDG≌△CEF；
(2) 设△ABC的边长为2，请你帮小聪求出正方形的边长．（结果精确到十分位）
(3) 小颖想：不求正方形的边长我也能画出正方形．具体作法是：如图3
①在AB边上任取一点G′，如图作正方形G′D′E′F′；
②连接BF′并延长交AC于F；
③作FE∥F′E′交BC于E，FG∥F′G′交AB于G，GD∥G′D′交BC于D，则四边形DEFG即为所求．你认为小颖的作法正确吗？请说明理由．