如图所示,木块质量 ,它以速度
,它以速度 水平地滑上一辆静止的平板小车,已知小车质量
水平地滑上一辆静止的平板小车,已知小车质量 ,木块与小车间的动摩擦因数为
,木块与小车间的动摩擦因数为 ,木块没有滑离小车,地面光滑,g取10
,木块没有滑离小车,地面光滑,g取10 ,求:
,求:
①木块相对小车静止时小车的速度的大小;
②从木块滑上小车到木块相对于小车刚静止时,小车移动的距离.
在光滑的地面上,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以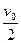 的速率弹回,而B球以
的速率弹回,而B球以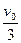 的速率向右运动,求
的速率向右运动,求
(1)A、B两球的质量之比;
(2)请你判断该碰撞是否为弹性碰撞。
为了安全,在公路上行驶的汽车之间应保持必要的距离,已知某高速公路的最高限速为108 km/h假设前方车辆突然停止,后车司机从发现这一情况经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s,刹车时汽车加速度的大小为5m/s2,该高速公路上汽车间的距离至少应为多少?
水滴自屋檐由静止落下,经过高为1.8米的窗口历时0.2秒,若空气阻力不计,屋檐离窗顶多高?(g=10m/s2)
一质点做匀加速直线运动,经4 s通过的位移是24 m,速度达到11 m/s,,求质点运动的初速度和加速度。
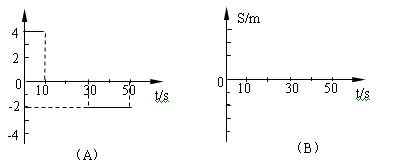
如图(A)所示是一个做直线运动的物体的速度图象。请在(B)中画出该物体运动的位移图像。