普朗克常量h=6.63×10-34 J·s,铝的逸出功W0=6.72×10-19 J,现用波长λ=200 nm的光照射铝的表面(结果保留三位有效数字).
(1)求光电子的最大初动能;
(2)若射出的一个具有最大初动能的光电子正对一个原来静止的电子运动,求在此运动过程中两电子电势能增加的最大值(电子所受的重力不计).
如图所示,A为电解槽,N为电炉子,恒定电压U=12 V,电解槽内阻rA=2 Ω,当S1闭合、S2断开时,电流表的示数为6 A;当S2闭合、S1断开时,电流表的示数为4 A,求:
(1)电炉子的电阻及发热功率各多大?
(2)在电解槽工作时,电能转化为化学能的功率为多少?
绝缘光滑水平面内有一圆形有界匀强电场,其俯视图如图所示,图中xOy所在平面与光滑水平面重合,场强方向与x轴正向平行,电场的半径为 m,圆心O与坐标系的原点重合,场强E="2" N/C,一带电荷量为
m,圆心O与坐标系的原点重合,场强E="2" N/C,一带电荷量为 C,质量
C,质量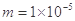 kg的带负电的粒子,由坐标原点O处以速度
kg的带负电的粒子,由坐标原点O处以速度 m/s沿y轴正方向射入电场,求:
m/s沿y轴正方向射入电场,求:
(1)粒子在电场中运动的时间;
(2)粒子出射点的位置坐标;
(3)粒子射出时具有的动能
如图所示,电源电动势为3 V,内阻不计,导体棒质量60 g,长1 m,电阻1.5 Ω,匀强磁场竖直向上,B=0.4 T.当开关S闭合后,棒从固定的光滑绝缘环的底端上滑到某一位置静止,试求在此位置上棒对每只环的压力为多少?若已知绝缘环半径0.5 m,求此位置与环底高度差为多少?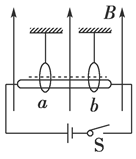
如图所示,光滑竖直绝缘杆与一圆周交于B.C两点,圆心固定并有电量为+Q的点电荷,一质量为m,电量为+q的环从杆上A点由静止释放.已知AB=BC=h, q<<Q,环沿绝缘杆滑到B点时的速度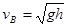 ,求A.C两点间的电势差及环达C点时的速度。
,求A.C两点间的电势差及环达C点时的速度。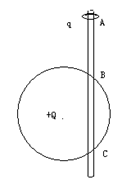
一个底面粗糙、质量为M的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成30°角;现用一端固定的轻绳系一质量为m的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为30°,如图所示,求: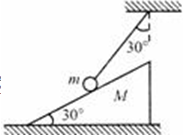
(1)当劈静止时绳子的拉力大小.
(2)若地面对劈的最大静摩擦力等于地面对劈支持力的k倍,为使整个系统静止,k值必满足什么条件?