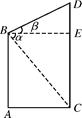
如图1，在等腰梯形ABCD中，AB∥CO，E是AO的中点，过点E作EF∥OC交BC于F，AO=4，OC=6，∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中，使点O与原点重合，OC在x轴正半轴上，点A、B在第一象限内。
（1） 求点E的坐标；
（2） 点P为线段EF上的一个动点，过点P作PM⊥EF交OC于点M，过M作MN∥AO交折线ABC于点N，
连结PN。设PE=x.△PMN的面积为S。
① 求S关于x的函数关系式；
② △PMN的面积是否存在最大值，若不存在，请说明理由。若存在，求出面积的最大值；
（3）另有一直角梯形EDGH（H在EF上，DG落在OC上，∠EDG=90°，且DG=3，HG∥BC）。现在开始操作：固定等腰梯形ABCO，将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动，直到点D与点C重合时停止（如图2）。设运动时间为t秒，运动后的直角梯形为E′D′G′H′;探究：在运动过程中，等腰梯形ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式。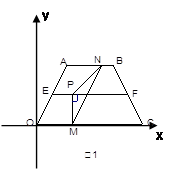
（1）|－3|－(π－3)0+2sin30°；
（2）已知：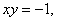
求代数式
的值．
已知抛物线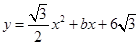 
经过A（2，0）． 设顶点为点P，与x轴的另一交点为点B．
（1）求b的值和点P、B的坐标；
（2）如图，在直线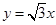
上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；
（3）在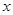
轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在,试举例验证你的猜想；如果不存在，试说明理由．
如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．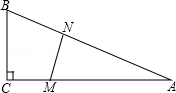
（1）求线段AB的长.
（2）当t为何值时，∠AMN=∠ANM？
（3）当t为何值时，△AMN的面积最大？并求出这个最大值．
甲、乙两公司参与一项治理大气净化工程，如果两公司合做，12天可以完成；如果两公司单独完成此项公程，乙公司所用时间是甲公司的1.5倍。
（1）甲、乙公司单独完成此项工程，各需多少天？
（2）已知这项工程甲、乙两公司合做共需付施工费102 000元，乙公司每天的施工费比甲公司每天的施工费少1500元. 若让一个公司单独完成这项工程，哪个公司施工费较少？
如图，两座建筑物AB及CD，其中A，C距离为50米，在AB的顶点B处测得CD的顶部D的仰角β＝30°，测得其底部C的俯角α＝60°，求两座建筑物AB及CD的高度(精确到0.1米)．