如图（a）所示，一端封闭的两条平行光滑导轨相距L，距左端L处的中间一段被弯成半径为H的1/4圆弧，导轨左右两段处于高度相差H的水平面上。圆弧导轨所在区域无磁场，右段区域存在磁场B0，左段区域存在均匀分布但随时间线性变化的磁场B（t），如图（b）所示，两磁场方向均竖直向上。在圆弧顶端，放置一质量为m的金属棒ab，与导轨左段形成闭合回路，从金属棒下滑开始计时，经过时间t0滑到圆弧顶端。设金属棒在回路中的电阻为R，导轨电阻不计，重力加速度为g。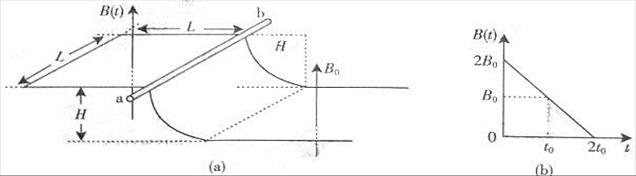
⑴问金属棒在圆弧内滑动时，回路中感应电流的大小和方向是否发生改变？
⑵求0到时间t0内，回路中感应电流产生的焦耳热量。
⑶若要使金属棒滑到圆弧底端进入匀强磁场B0的一瞬间，回路中感应电流恰好为零，各已知量之间应该满足什么关系？
如图9所示，一带电为q、质量为m的小物块放在一倾角为θ的光滑绝缘斜面上，当整个装置处于一水平向左的匀强电场中时，小物块恰好处于静止状态。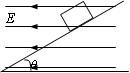
（1）试在答题卷的方框中分析小物块带的电荷种类。
（2）对物块进行受力情况，在受力分析图中标上符号，并在答题卷的相应位置写上各力的名称；
（3）求出该匀强电场的电场强度E的大小。
如图所示，将电动势E=1．5V、内阻r=0．5Ω的电源，与一粗细均匀的电阻丝相连，电阻丝的长度L=0．3m，电阻R=100Ω，当滑动片以v=5×10－3m·s-1的速度向右滑动时，电流表G的读数为多少？并指出电流表的正负极，已知电容器的电容C=2μF。
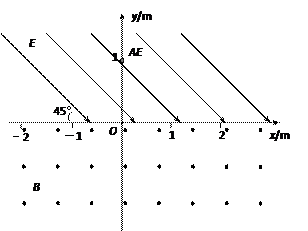在如图所示的直角坐标中，x轴的上方有与x轴正方向成45°角的匀强电场，场强的大小为E＝
×104V/m。x轴的下方有垂直于xOy面的匀强磁场，磁感应强度的大小为 B＝1×10－2T。把一个比荷为
C/kg的正电荷从y轴上坐标为（0，1）的A点处由静止释放。电荷所受的重力忽略不计，求：
（1）电荷从释放到第一次进入磁场时所用的时间t；
（2）电荷在磁场中的偏转半径；
（3）电荷第三次到达x轴上的位置。
一不计重力的带电粒子质量为m，电量为+q，经一电压为U1平板电容器C1加速后，沿平行板电容器C2两板的中轴进入C2，恰好从C2下边缘射出。C2两板间电压为U2，长为L，如图所示。求平行板电容器C2上下两极板间距离d=？
已知O、A、B、C为同一直线上的四点、AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发，沿此直线做匀速运动，依次经过A、B、C三点，已知物体通过AB段与BC段所用的时间相等。求O与A的距离．