(22分)如图（a），小球甲固定于水平气垫导轨的左端，质量m=0.4kg的小球乙可在导轨上无摩擦地滑动，甲、乙两球之间因受到相互作用而具有一定的势能，相互作用力沿二者连线且随间距的变化而变化。现已测出势能随位置x的变化规律如图（b）中的实线所示。已知曲线最低点的横坐标x0=20cm，虚线①为势能变化曲线的渐近线，虚线②为经过曲线上某点的切线。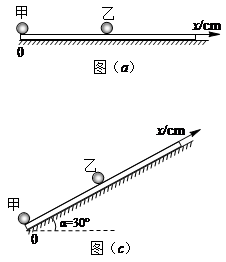
（1）将小球乙从x1=8cm处由静止释放，小球乙所能达到的最大速度为多大？
（2）假定导轨右侧足够长，将小球乙在导轨上从何处由静止释放，小球乙不可能第二次经过x0=20cm的位置？并写出必要的推断说明；
（3）若将导轨右端抬高，使其与水平面的夹角α=30°，如图(c)所示。将球乙从x2=6cm处由静止释放，小球乙运动到何处时速度最大？并求其最大速度；
（4）在图(b)上画出第（3）问中小球乙的动能Ek与位置x的关系图线。
如图所示是一种折射率
的棱镜。现有一束光线沿MN方向射到棱镜的AB面上，入射角的大小i＝60°，求：
（1）光在棱镜中传播的速率；
（2）画出此束光线进入棱镜后又射出棱镜的光路图，要求写出简要的分析过程。
如图所示是一列沿x轴正方向传播的简谐横波在t＝0时刻的波形图（波恰好传到x＝2m的质点处），已知波的传播速度v＝2m/s.
（1）请写出质点O简谐运动的表达式；
（2）求x＝3. 5m的质点P（图中没有画出）第二次到达波谷所需的时间。
(10分)A、B为一平行板，板长为l，两板间距离为d，板间区域内充满着匀强磁场，磁感应强度大小为B，方向垂直纸面向里。一个质量为m，带电荷量 为+q的带电粒子以一定初速度沿A、B两板中线且垂直于磁感线方向射入磁场中，粒子恰好从A板的右边界飞出。粒子重力不计。求：
(1)粒子在磁场中运动的轨道半径r和射入磁场的初速度v0各是多少？
(2)粒子在磁场中运动的时间t是多少？
(12分)如图所示，质量为m，电荷量为e的电子，从A点以速度v0垂直于电场方向射入一个电场强度为E的匀强电场中，从B点射出电场时的速度方向与电场线成120°角，电子重力不计。求：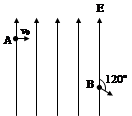
(1)电子在电场中的加速度大小a及电子在B点的速度大小vB?
(2)A、B两点间的电势差UAB?
(3)电子从A运动到B的时间tAB?
如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为L＝0.2米，在导轨的一端接有阻值为R＝0.5欧的电阻，在
0处有一与水平面垂直的均匀磁场，磁感强度B＝0.5T，一质量为m＝0.1千克的金属杆垂直放置在导轨上，并以v0＝2米／秒的初速度进入磁场，在安培力和一垂直于杆的水平外力F的共同作用下做匀变速直线运动，加速度大小为a＝2米／秒2、方向与初速度方向相反，设导轨和金属杆的电阻都可以忽略，且接触良好，求：
（1）电流为零时金属杆所处的位置；
（2）电流为最大值的一半时施加在金属杆上外力F的大小和方向；
（3）保持其它条件不变，而初速度v0取不同值，求开始时F的方向与初速度v0取值的关系。