以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是 的切线,连接OQ.求
的切线,连接OQ.求 的大小;
的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被 截得的弦长.
截得的弦长.
先化简: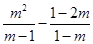 ,再选取一个适当的m的值代入求值.
,再选取一个适当的m的值代入求值.
在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记 ,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
抛物线 ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线 交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线
交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线 (
( )交边AB于点N.若△OAN的面积是4,求△OMN的面积.
)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
先化简,再求值: ,其中
,其中 ,
, .
.