如图,已知直线 的图象与
的图象与 轴、
轴、 轴交于
轴交于 、
、 两点。
两点。
(1)求点 、点
、点 的坐标和△
的坐标和△ 的面积。
的面积。
(2)求线段 的长。
的长。
(3)若直线l经过原点,与线段 交于点
交于点 (
( 为一动点),把△
为一动点),把△ 的面积分成2︰1两部分,求直线L的解析式。
的面积分成2︰1两部分,求直线L的解析式。
(本题满 分7分)
分7分) 
如图,已知二次函数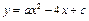 的图象与坐标轴交于点A(-1, 0)和点C(0,-5).
的图象与坐标轴交于点A(-1, 0)和点C(0,-5).
(1)求该二次函数的解析式和它与x轴的另一个交点B的坐标。
(2)在上面所求二次函数的对称轴上存在一点P(2,-2),连结OP,找出x轴上所有点M的坐标,使得△OPM是等腰三角形.
(1)如图①两个正方形的边长均为3,求三角形DBF的面积.
(2)如图②,正方形ABCD的边长为3,正方形CEFG的边长为1, 求三角形DBF的面积.
(3)如图③,正方形ABCD的边长为a,正方形CEFG的边长为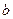 ,求三角形DBF的面积.
,求三角形DBF的面积. 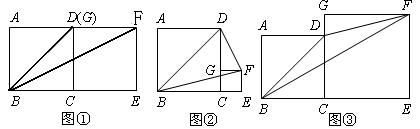
从上面计算中你能得到什么结论.
结论是:
(没写结论也不扣分)
如图,已知二次函数y = x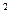 -4x + 3的图象交x轴于A、B两点(点A在点B的左侧)抛物线y = x
-4x + 3的图象交x轴于A、B两点(点A在点B的左侧)抛物线y = x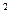 -4x + 3交y轴于点C,
-4x + 3交y轴于点C,
(1)求线段BC所 在直线的解析式.
在直线的解析式.
(2)又已知反比例函数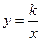 与BC有两个交点且k为正整数,求
与BC有两个交点且k为正整数,求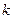 的值.
的值.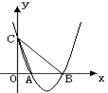
某校九年级两个班各为红十字会捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%.请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程.
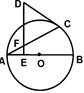
如图,已知AB为⊙O的直径,DC切⊙O于点C,过D点作DE⊥AB,垂足为E,DE交AC于点F. 求证:△DFC是等腰三角形.