如图,在直角梯形ABCD中,AD∥BC,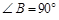 ,AD = 6,BC = 8,
,AD = 6,BC = 8,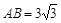 ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
(2)当BP = 1时,求△EPQ与梯形ABCD重叠部分的面积.
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
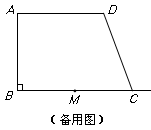
先化简,再求值:(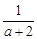 -1)¸
-1)¸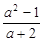 ,其中a=
,其中a=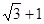 .
.
先化简: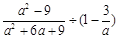 .若结果等于
.若结果等于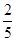 ,求出相应a的值.
,求出相应a的值.
如图,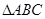 中,
中,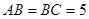 ,
,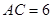 ,过点
,过点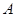 作
作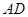 ∥
∥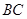 ,点
,点 、
、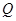 分别是射线
分别是射线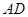 、线段
、线段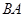 上的动点,且
上的动点,且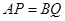 ,过点
,过点 作
作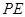 ∥
∥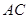 交线段
交线段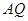 于点
于点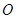 ,联接
,联接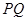 ,设
,设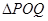 面积为
面积为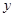 ,
,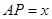 .
.
(1)用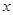 的代数式表示
的代数式表示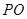 ;
;
(2)求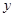 与
与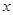 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接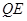 ,若
,若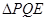 与
与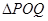 相似,求
相似,求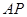 的长.
的长.
解下列一元二次方程:
(1)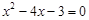 ; (2)
; (2)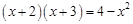 .
.
如图所示,△ABC中,∠A=96°。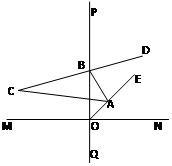
(1)BA1平分∠ABC,CA1平分∠ACD,请你求∠A1的度数;
(2)BA2平分∠A1BC,CA2平分∠A1CD,请你求∠A2的度数;
(3)依次类推,写出∠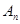 与∠
与∠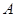 的关系式。
的关系式。
(4)小明同学用下面的方法画出了α角:作两条互相垂直的直线MN、PQ,垂足为O,作∠PON的角平分线OE,点A、B分别是OE、PQ上任意一点,再作∠ABP的平分线BD,BD的反向延长线交∠OAB的平分线于点C,那么∠C就是所求的α角,则α的度数为.