如图12－1－10所示， A、B两物体的质量都为m，拉A物体的细线与水平方向的夹角为30°时处于静止状态，不考虑摩擦力，设弹簧的劲度系数为k.若悬线突然断开后，A在水平面上做周期为T的简谐运动，当B落地时，A恰好将弹簧压缩到最短，求：
(1)A振动时的振幅；
(2)B落地时的速度．
如图所示，电阻R="10" W，电动机M的线圈电阻r="0.5" W，A、B间所加电压U="100" V，电流表示数I="30" A，则：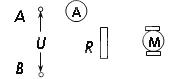
（1）流过电动机M的电流为多大？
（2）在1 min时间内，电动机输出的机械能为多少？
（3）如果在电动机正常工作时，转子突然被卡住，电动机的发热功率是多大？
如图所示的电路中，电源电动势E=6.0V，其内阻可忽略不计。电阻的阻值分别为
，电容器的电容
。闭合开关S，待电流稳定后，用电压表测
两端电压，其稳定值为
。
（1）该电压表的内阻为多大？
（2）由于电压表的接入，电容器的带电量变化了多少？
．如图所示，水平面上有一个动力小车，在动力小车上竖直固定着一个长度L1、宽度L2的矩形线圈，线圈匝线为n，总电阻为R，小车和线圈的总质量为m，小车运动过程所受摩擦力为f。小车最初静止，线圈的右边刚好与宽为d（d﹥L1）的有界磁场的左边界重合。磁场方向与线圈平面垂直，磁感应强度为B。现控制动力小车牵引力的功率，让它以恒定加速度a进入磁场，线圈全部进入磁场后，开始做匀速直线运动，直至完全离开磁场，整个过程中，牵引力的总功为W。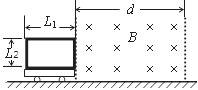
（1）求线圈进入磁场过程中，感应电流的最大值和通过导线横截面的电量。
（2）求线圈进入磁场过程中，线圈中产生的焦耳热。
（3）写出整个过程中，牵引力的功率随时间变化的关系式。
(10分)如图所示，水平方向的匀强电场场强为E，场区宽度为L，竖直方向足够长，紧挨着电场的是垂直于纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B。一个质量m，电荷量为q的带正电粒子，其重力不计，从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过时间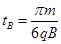
穿过中间磁场，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面。求：
(1)中间场区的宽度d；
(2)粒子从a点到b点所经历的时间
；
(3)当粒子第n次返回电场的MN边界时与出发点之间的距离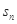
。
(10分)如图10所示，半径为R的四分之一圆弧形支架竖直放置，圆弧边缘C处有一小定滑轮，绳子不可伸长，不计一切摩擦，开始时，m1、m2两球静止，且m1＞m2，试求：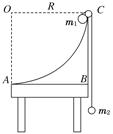
(1)m1释放后沿圆弧滑至最低点A时的速度．
(2)为使m1能到达A点，m1与m2之间必须满足什么关系．
(3)若A点离地高度为2R，m1滑到A点时绳子突然断开，则m1落地点离A点的水平距离是多少？