化简:[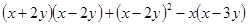 ]÷
]÷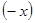
两种移动电话记费方式表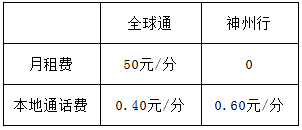
(1)一个月内本地通话多少分钟时,两种通讯方式的费用相同?
(2)若某人预计一个月内使用本地通话费180元,则应该选择哪种通讯方式较合算?
如图:线段AB=20cm,点C是线段AB上一点,点M是线段BC的中点,点N是线段AB的中点且BM=4cm,求线段NC的长.
一张方桌由一个桌面和四条桌脚组成,如果一立方米木材可制作方桌的桌面50个,或制作桌腿300条,现有5立方米木料,那么用多少木料做桌面,用多少木料做桌腿,恰好配成方桌多少张?
关于x、y的多项式mx3+3nxy2+2x3﹣xy2+2x2+4不含三次项,求2m+3n的值.
解方程
(1)2(3x﹣4)=4x﹣7(4﹣x)
(2) ﹣
﹣ =
= .
.