(本小题满分12分)
已知 =(cos
=(cos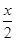 +sin
+sin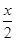 ,-sin
,-sin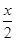 ),
), =(cos
=(cos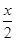 -sin
-sin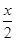 ,2cos
,2cos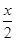 ).
).
(1)设f(x)= ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈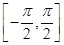 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
(本小题满分12分)
已知 均在椭圆
均在椭圆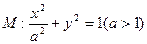 上,直线
上,直线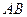 、
、 分别过椭圆的左右焦点
分别过椭圆的左右焦点 、
、 ,当
,当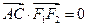 时,有
时,有 .
.
(I)求椭圆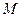 的方程;
的方程;
(II)设P是椭圆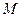 上的任一点,
上的任一点,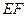 为圆
为圆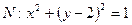 的任一条直径,求
的任一条直径,求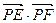 的最大值.
的最大值.
(本小题满分12分)
在四棱锥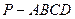 中,
中,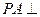 平面
平面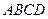 ,底面
,底面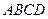 为矩形,
为矩形,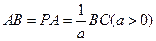 .
.
(I)当 时,求证:
时,求证: ;
;
(II)若 边上有且只有一个点
边上有且只有一个点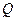 ,使得
,使得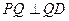 ,求此时二面角
,求此时二面角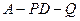 的余弦值.
的余弦值.
(本小题满分12分)
在 中,
中,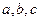 分别是
分别是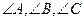 的对边长,已知
的对边长,已知 .
.
(I)若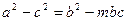 ,求实数
,求实数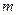 的值;
的值;
(II)若 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分12分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为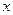 、
、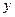 ,设
,设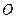 为坐标原点,点
为坐标原点,点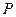 的坐标为
的坐标为 ,记
,记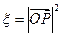 .
.
(I)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(II)求随机变量 的分布列和数学期望.
的分布列和数学期望.
某单位决定投资3 200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米造价45元,屋顶每平方米造价20元,试计算:
(1)仓库面积S的最大允许值是多少?
(2)为使S达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?