某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产记为正、减产记为负）：
（1）根据记录的数据可知星期四生产自行车多少辆？
（2）根据记录的数据可知本周实际生产自行车多少辆？
（3）产量最多的一天比产量最少的一天多生产自行车多少辆？
（4）该厂实行每周计件工资制，每生产一辆可得60元，若超过部分每辆另奖15元，少生产一辆扣20元，那么该厂工人这一周的工资总额是多少？
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+5 |
-2 |
-4 |
+13 |
-10 |
+16 |
-9 |
如图，△ABC是等腰三角形，AB=AC，请你用尺规作图将△ABC分成两个全等的三角形，并说明这两个三角形全等的理由．（保留作图痕迹，不写作法）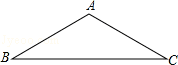
计算：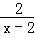
﹣
．
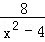阅读理解
抛物线y=
x2上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．
问题解决
如图，在平面直角坐标系中，直线y=kx+1与y轴交于C点，与函数y=x2的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．
（1）写出点C的坐标，并说明∠ECF=90°；
（2）在△PEF中，M为EF中点，P为动点．
①求证：PE2+PF2=2（PM2+EM2）；
②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．
（1）如图1是某个多面体的表面展开图．
①请你写出这个多面体的名称，并指出图中哪三个字母表示多面体的同一点；
②如果沿BC、GH将展开图剪成三块，恰好拼成一个矩形，那么△BMC应满足什么条件？（不必说理）
（2）如果将一个三棱柱的表面展开图剪成四块，恰好拼成一个三角形，如图2，那么该三棱柱的侧面积与表面积的比值是多少？为什么？（注：以上剪拼中所有接缝均忽略不计）
某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的而积最大？下面是两位学生争议的情境：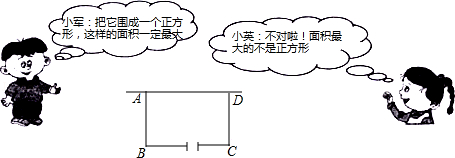
请根据上面的信息，解决问题：
（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；
（2）请你判断谁的说法正确，为什么？