已知:点A、B在数轴上分别表示 、
、
⑴ 对照数轴填写下表:
 |
6 |
—6 |
—6 |
—6 |
2 |
—1.5 |
 |
4 |
0 |
4 |
—4 |
—10 |
—1.5 |
| A、B两点的距离d |
|
|
|
|
|
|
⑵ 若A、B两点间的距离记为 ,试问
,试问 和
和 、
、 有何数量关系?
有何数量关系?
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(﹣2,4),B(﹣2,1),C(﹣5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1.
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2,得到对应的点A2,B2,C2,请画出△A2B2C2.
(3)求△A1B1C1与△A2B2C2的面积比.
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯的高度AB等于多少呢?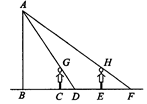
小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
解方程: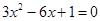
如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PCO=∠POC?若存在,求出符合条件的点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;