如图，在平面直角坐标系中，二次函数
的图像经过点
，
，
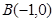，顶点为
．
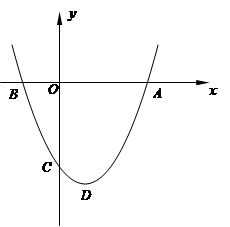
（1）求这个二次函数的解析式及顶点坐标；
（2）在
轴上找一点
（点与点
不重合），使得
，求点坐标；
（3）在（2）的条件下，将
沿直线
翻折，得到
，求点
坐标．
阅读理解： 对非负实数x“四舍五入”到个位的值记为<x>，
即：当n为非负整数时，如果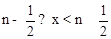
，则<x>＝n。
如：<0>＝<0.49>＝0，<0.64>＝<1.393>＝1，<3>＝3，<2.5>＝<3.12>＝3，…
试解决下列问题：
（1）填空：如果<3x－2>＝4，则实数x的取值范围为 ；
（2）当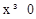
，m为非负整数时，求证：
；
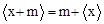（3）求满足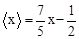
的所有非负实数x的值；
某校为了丰富学生的校园生活，准备购进一批价格分别为80元、60元的篮球和足球。该校打算用1000元购买篮球和足球，问恰好用完1000元，并且篮球、足球都买有的购买方案有哪几种？
已知 x1、x2是一元二次方程
的两个实数根。
（1）求
的取值范围；
（2）是否存在实数，使
成立？若存在，求出的值；若不存在，请说明理由。
定义一种新运算：观察下列各式：
1⊙3="1×4+3=7" ；3⊙（－1）= 3×4－1=11；5⊙4="5×4+4=24" ；4⊙（－3）= 4×4－3=13
（1）请你想一想：a⊙b=___________；
（2）若a≠b,那么a⊙b______b⊙a(填入 “=”或 “≠ ”) ；
（3）若a⊙(－2b) = 4，请计算 (a－b)⊙(2a+b)的值．
实数x、y、z、w满足x≥y≥z≥w≥0，且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.