函数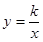 和
和
 的图像关于
的图像关于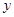 轴对称,我们把函数
轴对称,我们把函数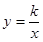 和
和
 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数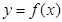 和
和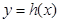 的图像关于
的图像关于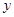 轴对称,那么我们就把函数
轴对称,那么我们就把函数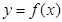 和
和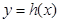 叫做互为“镜子”函数.
叫做互为“镜子”函数.
(1)请写出函数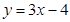 的“镜子”函数: ,
的“镜子”函数: ,
(2)函数 的“镜子”函数是 ;
;
(3)如图7,一条直线与一对“镜子”函数 (
(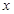 >
>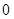 )和
)和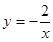 (
(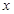 <
<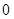 )的图像分别交于点
)的图像分别交于点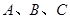 ,如果
,如果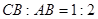 ,点
,点 在函数
在函数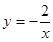 (
(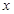 <
<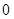 )的“镜子”函数上的对应点的横坐标是
)的“镜子”函数上的对应点的横坐标是 ,求点
,求点 的坐标.
的坐标. 
如图,已知抛物线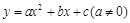 经过
经过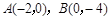 ,
,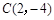 三点,且与
三点,且与 轴的另一个交点为
轴的另一个交点为 .
.
(1)求抛物线的解析式;
(2)用配方法求抛物线的顶点 的坐标和对称轴;
的坐标和对称轴;
(3)求四边形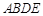 的面积.
的面积.
已知抛物线 与直线
与直线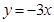 相交于点
相交于点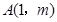 .
.
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到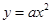 的图象?
的图象?
(3)设抛物线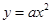 上依次有点
上依次有点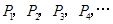 ,其中横坐标依次是
,其中横坐标依次是 ,纵坐标依次为
,纵坐标依次为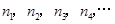 ,试求
,试求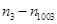 的值.
的值.
抛物线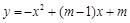 与
与 轴交于
轴交于 点.
点.
(1)求出 的值并画出这条抛物线;
的值并画出这条抛物线;
(2)求它与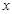 轴的交点和抛物线顶点的坐标;
轴的交点和抛物线顶点的坐标;
(3)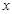 取什么值时,抛物线在
取什么值时,抛物线在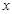 轴上方?
轴上方?
(4)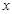 取什么值时,
取什么值时, 的值随
的值随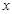 值增大而减小?
值增大而减小?
已知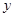 关于
关于 的函数:
的函数: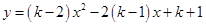 中满足
中满足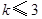 .
.
(1)求证:此函数图象与 轴总有交点.
轴总有交点.
(2)当关于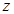 的方程
的方程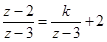 有增根时,求上述函数图象与
有增根时,求上述函数图象与 轴的交点坐标.
轴的交点坐标.
设二次函数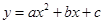 的图象开口向下,顶点在第二象限内.
的图象开口向下,顶点在第二象限内.
①确定a,b, 的符号;
的符号;
②若此二次函数的图象经过原点,且顶点的横坐标与纵坐标互为相反数,顶点与原点的距离为 ,求此二次函数的关系式.
,求此二次函数的关系式.