如图(1),BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F、G,连结FG,延长AF、AG,与直线BC相交于M、N。
(1)试说明:FG= (AB+BC+AC);
(AB+BC+AC);
(2)①如图(2),BD、CE分别是△ABC的内角平分线;②如图(3),BD为△ABC的内角平分线,CE为△ABC的外角平分线。
则在图(2)、图(3)两种情况下,线段FG与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况说明理由。
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.
已知:如图,在Rt△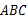 中,∠
中,∠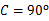 ,点
,点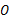 在
在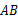 上,以
上,以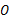 为圆心,
为圆心,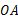 长为半径的圆与
长为半径的圆与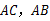 分别交于点
分别交于点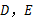 ,且∠
,且∠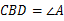 .判断直线
.判断直线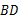 与
与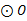 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.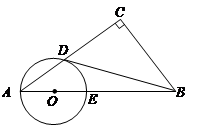
如图,△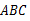 内接于
内接于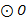 ,∠
,∠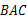 =
=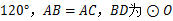 的直径,
的直径,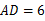 ,求
,求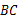 的长.
的长.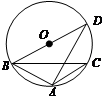
已知下列n(n为正整数)个关于x的一元二次方程: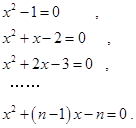
(1)请解上述一元二次方程;
(2)请你指出这n个方程的根具有什么共同特点,写出一条即可.