化简: 2
2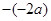 2
2
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
参考数据: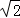 ≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.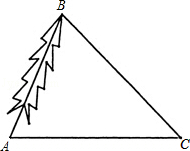
某公司为了解员工对“六五”普法知识的知晓情况,从本公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
| 组别 |
分数段/分 |
频数/人数 |
频率 |
| 1 |
50.5~60.5 |
2 |
a |
| 2 |
60.5~70.5 |
6 |
0.15 |
| 3 |
70.5~80.5 |
b |
c |
| 4 |
80.5~90.5 |
12 |
0.30 |
| 5 |
90.5~100.5 |
6 |
0.15 |
| 合计 |
40 |
1.00 |
(1)表中a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.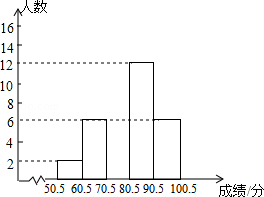
班级准备召开主题班会,现从由3名男生和2名女生所组成的班委中,随机选取两人担任主持人,求两名主持人恰为一男一女的概率.(请用“画树状图”或“列表”等方法写出过程)
如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.
解方程组: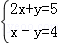 .
.