在平面直角坐标系中,已知抛物线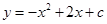 过点
过点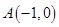 ;直线
;直线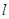 :
: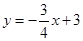 与
与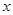 轴交于点
轴交于点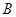 ,与
,与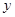 轴交于点
轴交于点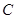 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点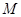 ;抛物线的顶点为
;抛物线的顶点为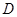 .
.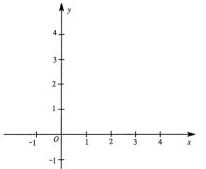
(1)求抛物线的解析式及顶点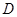 的坐标;
的坐标;
(2)过点 作
作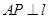 于点
于点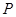 ,
,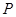 为垂足,求点
为垂足,求点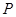 的坐标.
的坐标.
(3)若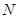 为直线
为直线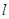 上一动点,过点
上一动点,过点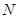 作
作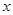 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点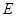 .问:是否存在这样的点
.问:是否存在这样的点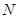 ,使得点
,使得点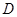 、
、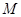 、
、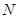 、
、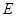 为顶点的四边形为平行四边形?若存在,求出点
为顶点的四边形为平行四边形?若存在,求出点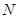 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(年甘肃兰州12分)如图,抛物线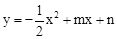 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).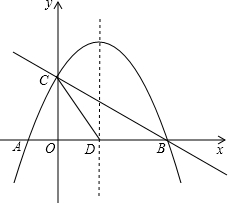
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
(年甘肃白银、定西、平凉、酒泉、临夏12分)如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.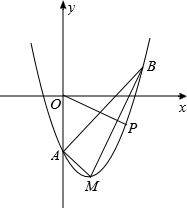
(年福建三明14分)如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(﹣2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;
(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.
(年福建莆田14分)如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
(1)如图1,若m= .
.
①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=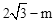 (0<m<
(0<m<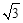 )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).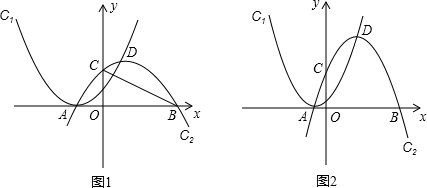
(年福建南平12分)如图,已知抛物线 图象经过A(﹣1,0),B(4,0)两点.
图象经过A(﹣1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.