在△ABC中,已知| |=4,|
|=4,| |=1,S△ABC=
|=1,S△ABC=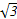 ,则
,则 ·
· 等于( )
等于( )
| A.-2 | B.2 | C.±4 | D.±2 |
设a,b是不共线的两个向量,其夹角是θ,若函数f(x)=(xa+b)·(a-xb)(x∈R)在(0,+∞)上有最大值,则( )
| A.|a|<|b|,且θ是钝角 |
| B.|a|<|b|,且θ是锐角 |
| C.|a|>|b|,且θ是钝角 |
| D.|a|>|b|,且θ是锐角 |
已知向量a,b满足|a|=|b|=2,a·b=0,若向量c与a-b共线,则|a+c|的最小值为( )
| A.1 | B. |
C.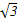 |
D.2 |
在△ABC中, =1,
=1, =2,则AB边的长度为( )
=2,则AB边的长度为( )
| A.1 | B.3 | C.5 | D.9 |
已知向量a=(cosθ,sinθ),b=( ,-1),则|2a-b|的最大值为( )
,-1),则|2a-b|的最大值为( )
A.4 |
B.4 | C.16 | D.8 |