古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
| A.13 = 3+10 | B.25 =" 9+16" | C.36 = 15+21 | D.49 = 18+31 |
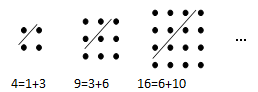
若把分式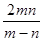 中的m ,n都扩大3倍,则分式的值()
中的m ,n都扩大3倍,则分式的值()
| A.不变 | B.扩大9倍 | C.扩大6倍 | D.扩大3倍 |
下列因式分解中,正确的是()
A.3m -6m=m(3m-6) -6m=m(3m-6) |
B.a b+ab+a=a(ab+b) b+ab+a=a(ab+b) |
C.-x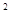 +2xy-y +2xy-y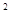 = -(x-y) = -(x-y)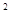 |
D.x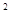 +y +y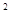 = (x+y) = (x+y)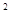 |
在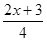 ,
,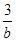 ,
,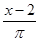 ,
,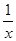 -y,
-y,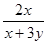 ,
,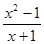 各式中,分式的个数为()
各式中,分式的个数为()
| A.2个 | B.3个 | C.4个 | D.5个 |
下列从左到右的变形,是因式分解的是()
A.(a+3)(a-3)=a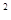 -9 -9 |
B.a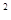 b+ab b+ab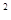 =ab(a+b) =ab(a+b) |
C.x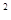 +x-5=(x-2)(x+3)+1 +x-5=(x-2)(x+3)+1 |
D.x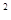 +1=x(x+ +1=x(x+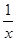 ) ) |
已知点A(2-a ,a +1)在第一象限,则a的取值范围是()
| A.a>2 | B.-1<a<2 | C.a<-1 | D.a<1 |