如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-4, 0），点B的坐标是（0, b）（b > 0）. P是直线AB上的一个动点，作 PC⊥x轴，垂足为C. 记点P关于y轴的对称点为P′（点P′不在y轴上），连结PP′，P′A，P′C. 设点P的横坐标为a,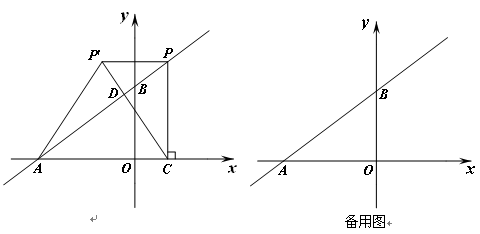
（1）当b=3时，
①求直线AB的解析式；
②若点P′ 的坐标是（-1，m）,求m的值；
（2）若点P在第一象限，记直线AB与P′C的交点为D. 当P′D:DC=1:3时，求a的值；
（3）若点P在第一象限，是否同时存在a，b，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由。
解下列方程：
（1）
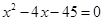
（2）x(x+3)=2x+6
展开你想象的翅膀，尽可能多地从方程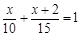
中猜想出它可能会是哪种类型的实际问题，将其编写出来，并解答之。
经营户小张在批发市场了解到以下信息内容：
| 蔬菜品种 |
红辣椒 |
黄瓜 |
西红柿 |
茄子 |
| 批发价(元/千克) |
4 |
1.2 |
1.6 |
1.1 |
| 零售价(元/千克) |
5 |
1.4 |
2.0 |
1.3 |
他共用116元钱从市场上批发了红辣椒和西红柿44千克到菜市场去卖，当天卖完，请你计算小张能赚多少钱？
为了节约开支和节约能源，某单位按以下规定收取每月的电费：用电不超过140度，按每度0.43元收费，如果超过140度，超过的部分按每度0.57元收费，若某用户11月份的电费平均每度0.5元，则该用户11月份应交电费多少元？
某车间有技术工人85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配成一套，问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套？并求出加工了多少套？