阅读下列材料,然后解答后面的问题。
我们知道方程 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由 ,得
,得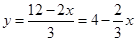 ,(
,( 、
、 为正整数)
为正整数)  则有
则有 .
.
又 为正整数,则
为正整数,则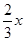 为正整数.
为正整数.
由2与3互质,可知: 为3的倍数,从而
为3的倍数,从而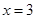 ,代入
,代入 .
. 的正整数解为
的正整数解为
问题:(1)请你写出方程 的一组正整数解:
的一组正整数解:
(2)若 为自然数,则满足条件的
为自然数,则满足条件的 值有 个
值有 个
| A.2 | B.3 | C.4 | D.5 |
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
计算: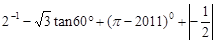
如图,Rt△AB ¢C ¢是由Rt△ABC绕点A顺时针旋转得到的,连结CC ¢交斜边于点E,CC ¢的延长线交BB ¢于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC= ,∠CAC ¢ =
,∠CAC ¢ =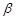 ,试探索
,试探索 、
、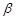 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.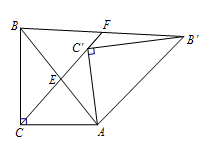
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?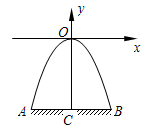
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由. 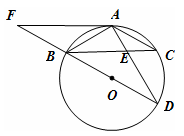
商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加件,每件商品盈利元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?