(12分)(2010·连云港模拟)如图9所示，B是质量为2m、半径为R的光滑半球形碗，放在光滑的水平桌面上．A是质量为m的细长直杆，光滑套管D被固定，A可以自由上下运动，物块C的质量为m，紧靠半球形碗放置．初始时，A杆被握住，使其下端正好与碗的半球面的上边缘接触(如图)．然后从静止开始释放A，A、B、C便开始运动．求：
(1)长直杆的下端运动到碗的最低点时，长直杆竖直方向的速度和B、C水平方向的速度；
(2)运动的过程中，长直杆的下端能上升到的最高点距离半球形碗底部的高度．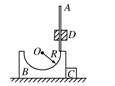
如图所示，小物块A在粗糙水平面上做直线运动，经距离
时与另一小物块B发生碰撞并粘在一起以速度v飞离桌面，最终落在水平地面上。已知=5.0m，s=0.9m，A、B质量相等且m=0.10kg，物块与桌面间的动摩擦因数µ=0.45，桌面高h=0.45m。不计空气阻力，重力加速度g=10m/s2。
求：（1）A、B一起平抛的初速度v；
（2）小物块A的初速度v0。
|
如右图所示，长
＝0.2 m的细线上端固定在O点，下端连接一个质量为m＝0.5kg的小球，悬点O距地面的高度H＝0.35m，开始时将小球提到O点而静止，然后让它自由下落，当小球到达使细线被拉直的位置时，刚好把细线拉断，再经过t＝0.1 s落到地面，如果不考虑细线的形变，g＝10 m/s2，试求：
(1)细线拉断前后的速度大小和方向；
(2)假设细线由拉直到断裂所经历的时间为
，试确定细线的平均张力大小．
在光滑水平面上，原来静止的物体在水平力F的作用下，经过时间ｔ、通过位移Ｌ后，动量为ｐ、动能为Ek ,则:
(1)若由静止出发，仍在水平力F的作用下，求经过时间2ｔ后物体的动能；
(2)若由静止出发，仍在水平力F的作用下，求通过位移2Ｌ后物体的动量。
如图（甲）示，光滑曲面MP与光滑水平面PN平滑连接，N端紧靠速度恒定的传送装置，PN与它上表面在同一水平面．小球A在MP上某点静止释放，与静置于PN上的工件B碰撞后，B在传送带上运动的v-t图象如图（乙）且t0已知，最后落在地面上的E点．已知重力加速度为g，传送装置上表面距地面高度为H．
（1）求B与传送带之间的动摩擦因数μ；
（2）求E点离传送装置右端的水平距离L；
（3）若A、B发生的是弹性碰撞且B的质量是A的2倍，要使B始终落在E点，试判断A静止释放点离PN的高度h的取值范围．
如图，匀强磁场垂直铜环所在的平面，导体棒a的一端固定在铜环的圆心O处，另一端紧贴圆环，可绕O匀速转动．通过电刷把铜环、环心与两竖直平行金属板P、Q连接成如图所示的电路，R1、R2是定值电阻．带正电的小球通过绝缘细线挂在两板间M点，被拉起到水平位置；合上开关K，无初速度释放小球，小球沿圆弧经过M点正下方的N点到另一侧．
已知：磁感应强度为B；a的角速度大小为ω，长度为l，电阻为r；R1=R2=2r，铜环电阻不计；P、Q两板间距为d；带电的质量为m、电量为q；重力加速度为g．求：
（1）a匀速转动的方向；
（2）P、Q间电场强度E的大小；
（3）小球通过N点时对细线拉力T的大小．