(15分)如图16甲所示,水平传送带的长度L=6 m,皮带轮以速度v顺时针匀速转动,现在一质量为1 kg的小物块(可视为质点)以水平速度v0从A点滑上传送带,越过B点后做平抛运动,其水平位移为x,保持物块的初速度v0不变,多次改变皮带轮的速度v依次测量水平位移x,得到如图16乙所示的x-v图象.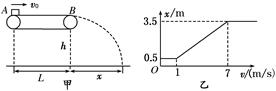
(1)当0<v≤1 m/s时,物块在A、B之间做什么运动?当v≥7 m/s时,物块在A、B之间做什么运动?
(2)物块的初速度v0多大?
如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103V/m。一不带电的绝缘小球甲,以速度υ0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞。已知乙球的质量为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,甲球质量为乙球质量的k倍,g取10m/s2。(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移) 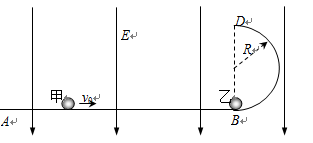
若k=1,且甲乙两球碰撞后,乙恰能通过轨道的最高点D,求甲的速度υ0;
若k>1,且甲仍以(1)中的速度υ0向右运动,求乙在轨道上的首次落点到B点的距离范围。
如图所示,相距为d、板间电压为U的平行金属板M、N间有垂直纸面向里、磁感应强度为B0的匀强磁场;在pOy区域内有垂直纸面向外磁感应强度为B的匀强磁场;pOx区域为无场区.一正离子沿平行于金属板、垂直磁场射入两板间并做匀速直线运动,从H(0,a)点垂直y轴进入第Ⅰ象限.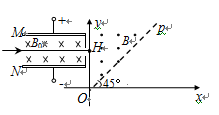
求离子在平行金属板间的运动速度;
若离子经Op上某点离开磁场,最后垂直x轴离开第Ⅰ象限,求离子在第Ⅰ象限磁场区域的运动时间;
要使离子一定能打在x轴上,则离子的荷质比
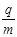 应满足什么条件?
应满足什么条件?
如图所示,光滑水平面上静止放着长L=1.6m,质量为M=3kg的木块(厚度不计),一个质量为m=1kg的小物体放在木板的最右端,m和M之间的动摩擦因数μ=0.1,今对木板施加一水平向右的拉力F,(g取10m/s2)
如果拉力F=10N恒定不变,求小物体离开木板时的动能大小?
为使物体与木板不发生滑动,F不能超过多少?
如图,A、B两点所在的圆半径分别为r1和r2,这两个圆为同心圆,圆心处有一带正电为+Q的点电荷,内外圆间的电势差为U。一电子仅在电场力作用下由A运动到B,电子经过B点时速度为v。若电子质量为m,带电量为e。求: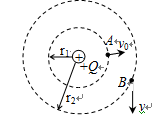
电子经过B点时的加速度大小。
电子在A点时的速度大小v0。
如图所示,一质量为m、电荷量为q、重力不计的微粒,从倾斜放置的平行电容器I的A板处由静止释放,A、B间电压为U1。微粒经加速后,从D板左边缘进入一水平放置的平行板电容器II,由C板右边缘且平行于极板方向射出,已知电容器II的板长为板间距离的2倍。电容器右侧竖直面MN与PQ之间的足够大空间中存在着水平向右的匀强磁场(图中未画出),MN与PQ之间的距离为L,磁感应强度大小为B。在微粒的运动路径上有一厚度不计的窄塑料板(垂直纸面方向的宽度很小),斜放在MN与PQ之间, =45°。求:
=45°。求:
微粒从电容器I加速后的速度大小;
电容器IICD间的电压;
假设粒子与塑料板碰撞后,电量和速度大小不变、方向变化遵循光的反射定律,碰撞时间极短忽略不计,微粒在MN与PQ之间运动的时间和路程。