已知命题：①“所有能被2整除的整数都是偶数”的否定是“所有能被2整除的整数不都是偶数”②“菱形的两条对角线互相垂直”的逆命题；③“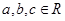
，若
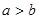，则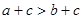
”的逆否命题；④“若
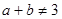，则
或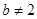
”的否命题． 上述命题中真命题的个数为（ ）
| A．1 | B．2 | C．3 | D．4 |
设
是定义在
上的奇函数，且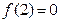
，则方程
在区间
的解的个数的最小值是（）
| A．4 | B．5 | C．6 | D．7 |
双曲线x2-y2=1的左焦点为F,过点F且斜率为k的直线l与双曲线左支上位于x轴下方(不包括与x轴的交点)有且仅有一个交点,则直线l的斜率k的取值范围是( )
A．(-∞,0)∪［1,+∞ |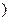
B．(-∞,0)∪(1,+∞) |
| C．(-∞,-1)∪［1,+∞ |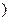
D．(-∞,-1)∪(1,+∞) |
设双曲线
-
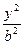=1的右支上有三点M、N、P,若这三点到右焦点的距离成等差数列,则它们的横坐标m、n、p( )
| A．必定成等差数列 | B．必定成等比数列 |
| C．既不成等差数列也不成等比数列 | D．有时成等差数列,有时成等比数列 |
椭圆
+
=1(m>n>0)和双曲线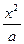
-
=1(a>0,b>0)有相同的焦点F1、F2,P是这两条曲线的一个交点,则|PF1|·|PF2|等于( )
| A．m-a | B． (m-a) |
C．m2-a2 | D． - |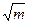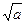
若k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
| A．焦点在x轴上的椭圆 | B．焦点在y轴上的椭圆 |
| C．焦点在y轴上的双曲线 | D．焦点在x轴上的双曲线 |