如图所示,多面体EF﹣ABCD中,底面ABCD为等腰梯形,AB∥CD,四边形ACFE为矩形,且平面ACFE⊥平面ABCD,AD=DC=BC=CF=1,AC⊥BC,∠ADC=120°
(1)求证:BC⊥AF
(2)求平面BDF与平面CDF所成夹角的余弦值. 
设函数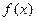 对任意
对任意 ,都有
,都有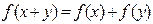 ,
,
且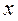 > 0时,
> 0时,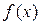 < 0,
< 0, .
.
(1)求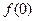 ;
;
(2)求证: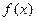 是奇函数;
是奇函数;
(3)请写出一个符合条件的函数;
(4)证明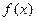 在R上是减函数,并求当
在R上是减函数,并求当 时,
时,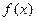 的最大值和最小值
的最大值和最小值
已知关于 的方程
的方程 (
( )有实根b
)有实根b
(1)求实数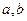 的值;
的值;
(2)若复数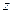 满足|
满足|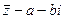 |-2|
|-2|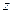 |=0,求
|=0,求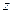 为何值时|
为何值时|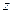 |有最小值,并求出|
|有最小值,并求出|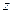 |的最小值。
|的最小值。
已知
求证:(1)
(2)| |、|
|、| |、|
|、|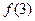 |中至少有一个不小于
|中至少有一个不小于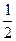
12分)某个服装店经营某种服装,在某周内获纯利 (元),与该周每天销售这种服装件数
(元),与该周每天销售这种服装件数 之间的一组数据关系见表:
之间的一组数据关系见表:
 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
 |
66 |
69 |
73 |
81 |
89 |
90 |
91 |
已知 ,
, ,
, .
.
(1)求 ;
;
(2)画出散点图;
(3)求出回归方程.
(参考公式:
 )
)
(1)计算
(2)复数 满足
满足 求复数
求复数
的对应点Z所在的象限。