如图（a）所示，两根足够长的水平平行金属导轨相距为L＝0.5 m，其右端通过导线连接阻值R＝0.6Ω的电阻，导轨电阻不计，一根质量为m＝0.2 kg、阻值r＝0.2Ω的金属棒ab放在两导轨上，棒与导轨垂直并保持良好接触，金属棒与导轨间的动摩擦因数m＝0.5。整个装置处在竖直向下的匀强磁场中，取g＝10m/s2。若所加磁场的磁感应强度大小恒为B，通过小电动机对金属棒施加水平向左的牵引力，使金属棒沿导轨向左做匀加速直线运动，经过0.5s电动机的输出功率达到P＝10W，此后电动机功率保持不变。金属棒运动的v～t图像如图（b）所示，试求：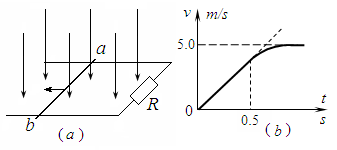 
（1）磁感应强度B的大小；
（2）在0～0.5s时间内金属棒的加速度a的大小；
（3）在0～0.5s时间内电动机牵引力F与时间t的关系；
（4）若在0～0.3s时间内电阻R产生的热量为0.15J，则在这段时间内电动机做的功。
如图所示为一利用传输带输送货物的装置．物块（视为质点）自平台经斜面滑到一以恒定速度v运动的水平长传输带上，再由传输带输送到远处目的地．已知斜面高h=2.0m，水平边长L=4.0m，传输带宽d=2.0m，传输带的运动速度v=3.0m/s，物块与斜面间的摩擦系数μ1=0.30，物块自斜面顶端下滑的初速度为零，沿斜面下滑的速度方向与传输带运动方向垂直．设物块通过斜面与传输带交界处时无动能损失．重力加速度g=10m/s2．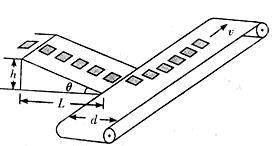
（1）为使物块滑到传输带上后不会从传输带边缘脱离，物块与传输带之间的摩擦系数μ2至少为多少？
（2）当货物的平均流量（单位时间里输送的货物质量）稳定在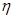
＝40kg/s时，求单位时间里物块对传输带所做的功W1以及传输带对物块所做功W2。
如图所示，地面和半圆轨道面均光滑。质量M =" 1kg" 、长L = 4m的小车放在地面上，其右端与墙壁的距离为S=3m，小车上表面与半圆轨道最低点P的切线相平。现有一质量m = 2kg的滑块（视为质点）以v0 = 6m/s的初速度滑上小车左端，带动小车向右运动。小车与墙壁碰撞时即被粘在墙壁上，已知滑块与小车表面的滑动摩擦因数μ =" 0.2" ，g取10m/s2。
（1）求小车与墙壁碰撞时的速度；
（2）要使滑块在半圆轨道上运动时不脱离，求半圆轨道的半径R的取值．
试将一天的时间记为T，地球半径记为R，地球表面重力加速度为g．（结果可保留根式）
（1）试求地球同步卫星P的轨道半径RP；
（2）若已知一卫星Q位于赤道上空且卫星Q运动方向与地球自转方向相反，赤道上一城市A的人平均每三天观测到卫星Q四次掠过他的上空，试求Q的轨道半径RQ
如图所示，在光滑的水平面上有一长为L的木板B，其右侧边缘放有小滑块C，与木板B完全相同的木板A以一定的速度向左运动，与木板B发生正碰，碰后两者粘在一起并继续向左运动，最终滑块C刚好没有从木板上掉下．已知木板A、B和滑块C的质量均为m，C与A、B之间的动摩擦因数均为μ．求：
①木板A与B碰前的速度v0；
②整个过程中木板B对木板A的冲量I．
如图甲所示，长木板B固定在光滑水平面上；可看做质点的物体A静止叠放在B的最左端，现用F=6N的水平力向右拉物体A，A经过5s运动到B的最右端，其v-t图象如图乙所示，已知A、B的质量分别为lkg和4kg，A、B间的最大静摩擦力等于滑动摩擦力．
（1）求物体A、B间的动摩擦因数；
（2）若B不固定，求A运动到B的最右端所用的时间．