如图所示,平行且足够长的两条光滑金属导轨,相距0.5 m,与水平面夹角为30°,不计电阻,广阔的匀强磁场垂直穿过导轨平面,磁感应强度B=0.4 T,垂直导轨放置两金属棒 和
和 ,长度均为0.5 m,电阻均为0.1Ω,质量分别为0.1 kg和0.2 kg,两金属棒与金属导轨接触良好且可沿导轨自由滑动。现
,长度均为0.5 m,电阻均为0.1Ω,质量分别为0.1 kg和0.2 kg,两金属棒与金属导轨接触良好且可沿导轨自由滑动。现 棒在外力作用下,以恒定速度ν=1.5m/s沿着导轨向上滑动,
棒在外力作用下,以恒定速度ν=1.5m/s沿着导轨向上滑动, 棒则由静止释放。试求:(取g="10" m/s2)
棒则由静止释放。试求:(取g="10" m/s2)
(1)金属棒 产生的感应电动势;
产生的感应电动势;
(2)闭合回路中的最小电流和最大电流;
(3)金属棒 的最终速度。
的最终速度。
在光滑的水平面上,质量为m1的小球A以速率v0向右运动。在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球质量之比m1/m2。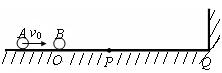
反射式速调管是常用的微波器械之一,它利用电子团在电场中的振荡来产生微波,其振荡原理与下述过程类似。如图所示,在虚线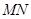 两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动。已知电场强度的大小分别是
两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动。已知电场强度的大小分别是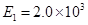 N/C和
N/C和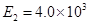 N/C,方向如图所示,带电微粒质量
N/C,方向如图所示,带电微粒质量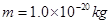 ,带电量
,带电量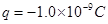 ,A点距虚线
,A点距虚线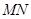 的距离
的距离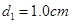 ,不计带电微粒的重力,忽略相对论效应。求:
,不计带电微粒的重力,忽略相对论效应。求: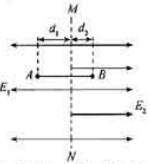
(1)B点到虚线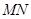 的距离
的距离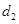 ;
;
(2)带电微粒从A点运动到B点所经历的时间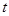 。
。
如图所示,坡道顶端距水平面高度为h,质量为m1的小物块A从坡道顶端由静止滑下,进入水平面上的滑道时无机械能损失,为使A制动,将轻弹簧的一端固定在水平滑道延长线M处的墙上,另一端与质量为m2的挡板B相连,弹簧处于原长时,B恰位于滑道的末端O点。A与B碰撞时间极短,碰后结合在一起共同压缩弹簧,已知在OM段A、B与水平面间的动摩擦因数均为μ,其余各处的摩擦不计,重力加速度为g,求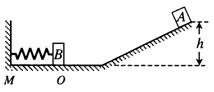
(1)物块A在与挡板B碰撞前瞬间速度v的大小;
(2)弹簧最大压缩量为d时的弹性势能EP(设弹簧处于原长时弹性势能为零)。
光滑水平面上放着质量mA="1" kg的物块A与质量mB="2" kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能Ep="49" J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R="0.5" m,B恰能到达最高点C。取g="10" m/s2,求:
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I的大小;
(3)绳拉断过程绳对A所做的功W。
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。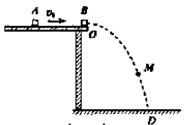
(1)已知滑块质量为m,碰撞时间为 ,求碰撞过程中A对B平均冲力的大小。
,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨迹完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。