如图,方格纸中,每个小正方形的边长都是1个单位长度,△ABC的三个顶点都在格点上.
(1)画出△ABC沿射线DE方向向下平移4个单位长度得到的△A1B1C1;
(2)画出△A1B1C1与绕点O逆时针旋转180°后得到的△A2B2C2;
(3)判断△ABC与△A2B2C2的是否关于某点成中心对称?若是在图中标出对称中心点P.
已知关于x,y的方程组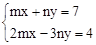 的解为
的解为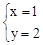 ,求m,n的值;
,求m,n的值;
化简: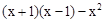
计算: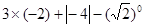
抛物线 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.
(2)如图2,AC:AB=1: ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值.