如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为(－3，0)、(0，4)，抛物线y＝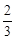
x2＋bx＋c经过点B，且顶点在直线x＝
上．
(1)求抛物线对应的函数关系式；
(2)若把△ABO沿x轴向右平移得到△DCE，点A、B、O的对应点分别是D、C、E，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
(3)在(2)的条件下，连接BD，已知对称轴上存在一点P使得△PBD的周长最小，求出P点的坐标；
(4)在(2)、(3)的条件下，若点M是线段OB上的一个动点(点M与点O、B不重合)，过点M作∥BD交x轴于点N，连接PM、PN，设OM的长为t，△PMN的面积为S，求S和t的函数关系式，并写出自变量t的取值范围，S是否存在最大值？若存在，求出最大值和此时M点的坐标；若不存在，说明理由．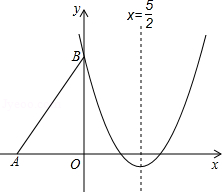
用适当的方法解下列方程
（1）
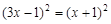
（2）用配方法解方程：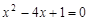
如图，在直角坐标系中，△ABC的顶点坐标分别为A（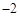
，5），B（
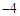，1）和C（
，3），作出△ABC关于原点O对称的△A1B1C1，并写出点A、B、C的对应点A1、B1、C1的坐标．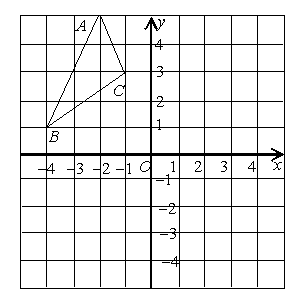
如图1，在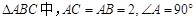
，将一块与
全等的三角板的直角顶点放在点C上，一直角边与BC重叠。
（1）操作1：固定，将三角板沿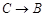
方向平移，使其直角顶点落在BC的中点M，如图2所示，探究：三角板沿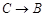方向平移的距离为___________；
（2）操作2：在（1）的情况下，将三角板BC的中点M顺时针方向旋转角度
，如图3所示，探究：设三角形板两直角边分别与AB、AC交于点P、Q，观察四边形MPAQ形状的变化，问：四边形MPAQ的面积S是否改变，若不变，求其面积；若改变，试说明理由；
（3）在（2）的情形下，连PQ，设
的面积为y，试求y关于x的函数关系式，并求x为何值时，y的值是四边形MPAQ的面积的一半，此时，指出四边形MPAQ的形状。
如图，正方形ABCD的长为1，点E是AD边上的动点且从点A沿AD向D运动，以BE为边，在BE的上方作正方形BEFG，为DC与EF的交点，请探索: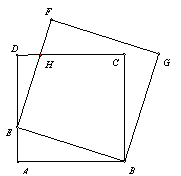
（1）连接CG，线段AE与CG是否相等? 请说明理由．
（2）设AE=x，CG=y，请确定y与x的函数关系式并说明自变量的取值范围．
（3）连接BH，当点E运动到边AD上的某一点时将有△BEH∽△BAE，请你指出这一点的位置，并说明理由．
为了贯彻落实国务院关于促进家电下乡的指示精神，有关部门自2007年12月底起进行了家电下乡试点，对彩电、冰箱（含冰柜）、手机三大类产品给予产品销售价格13%的财政资金直补．企业数据显示，截至2008年12月底，试点产品已销售350万台（部），销售额达50亿元，与上年同期相比，试点产品家电销售量增长了40%．
（1）求2007年同期试点产品类家电销售量为多少万台（部）？
（2）如果销售家电的平均价格为：彩电每台1500元，冰箱每台2000元，手机每部800元，已知销售的冰箱（含冰柜）数量是彩电数量的
倍，求彩电、冰箱、手机三大类产品分别销售多少万台（部），并计算获得的政府补贴分别为多少万元？