(本小题满分16分)
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.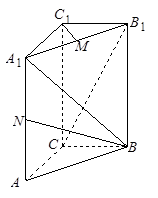
(1)求 的长;
的长;
(2)求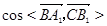 的值;
的值;
(3)求证:A1B⊥C1M.
已知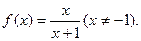
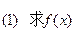 的单调区间;
的单调区间;
(2)若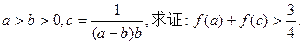
某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为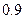 万元,年维修费用第一年是
万元,年维修费用第一年是 万元,以后逐年递增
万元,以后逐年递增 万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
已知函数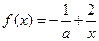 ,若
,若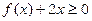 在(0,+
在(0,+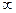 )上恒成立,求
)上恒成立,求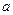 的取值范围。
的取值范围。
某乡为提高当地群众的生活水平,由政府投资兴建了甲、乙两个企业,2007年该乡从甲企业获得利润320万元,从乙企业获得利润720万元.以后每年上交的利润是:甲企业以1.5倍的速度递增,而乙企业则为上一年利润的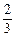 .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
(1)若以2007年为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题?
(2)试估算2015年底该乡能否达到小康水平?为什么?
【解题思路】经审题抽象出数列模型
.某建筑的金属支架如图所示,根据要求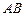 至少长2.8m,
至少长2.8m,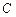 为
为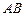 的中点,
的中点, 到
到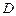 的距离比
的距离比 的长小0.5m,
的长小0.5m, ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计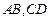 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?