△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲.乙两种剪法,哪种剪法所得的正方形面积大?请说明理由。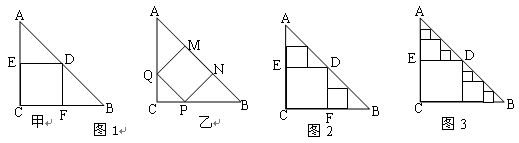
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为 ;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为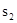 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为
;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为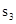 ,继续操作下去……,则第10次剪取时,
,继续操作下去……,则第10次剪取时, ;
;
(3)求第10次剪取后,余下的所有小三角形的面积之和。
若2m-4与3m-1是同一个数的两个平方根,求m的值
在平面直角坐标系xOy中,二次函数y=mx2+(m-3)x-3(m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
求点A的坐标;
当∠ABC=45°时,求m的值;
已知一次函数y=kx+b,点P(n,0)是x轴上的一个动点,在(2)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数y=mx2+(m-3)x-3(m>0)的图象于点N.若只有当-2<n<2时,点M位于点N的上方,求这个一次函数的解析式.(友情提示:自画图形)
如图,直线y=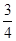 x-3分别与y轴、x轴交于点A,B,抛物线y=-
x-3分别与y轴、x轴交于点A,B,抛物线y=-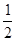 x2+2x+2与y轴交于点C,此抛物线的对称轴分别与BC,x轴交于点P,Q.
x2+2x+2与y轴交于点C,此抛物线的对称轴分别与BC,x轴交于点P,Q.
求证:AB=AC;
求证:AP垂直平分线段BC.
在小岛上有一观察站A.据测,灯塔B在观察站A北偏西45°的方向,灯塔C在B正东方向,且相距10海里,灯塔C与观察站A相距10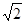 海里,请你测算灯塔C处在观察站A的什么方向?
海里,请你测算灯塔C处在观察站A的什么方向?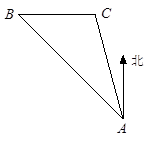
五月石榴红,枝头鸟儿歌. 一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处. 从A处看房屋顶部C处的仰角为30°,看房屋底部D处的俯角为45°,石榴树与该房屋之间的水平距离为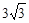 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.