已知抛物线y＝ax2＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB．OC的长（OB<OC）是方程x2－10x＋16＝0的两个根，且抛物线的对称轴是直线x＝－2．
（1）求A、B、C三点的坐标；
（2）求此抛物线的表达式；
（3）连接AC、BC，若点E是线段AB上的一个动点（与点A．点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；
（4）在（3）的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．
（本题8分）某班“2
011年新春联欢会”中，有一个摸奖游戏，规则如下：有4张纸牌，背面都是喜羊羊头像，正面有2张笑脸、 2张哭脸．现将4
张纸牌洗匀后背面朝上摆放到桌上，然后让同学去翻纸牌．
（1）现小芳有一次翻牌机会，若正面是笑脸的就获奖，正面是哭脸的不获奖．她从中随机翻开一张纸牌，小芳获奖的概率是．
（2）如果小芳、小明都有翻两张
牌的机会．小芳先翻一张，放回后再翻一张；小明同时翻开两张纸牌．他们翻开的两张纸牌中只要出现笑脸就获奖．他们获奖的机会相等吗？请说明理由．
（本题7分）某市光明中学全体学生积极参加“同心协力，抗震救灾”活动，
九年级甲班两位同学对本班捐款情况作了统计：全班50人共捐款900元，两位同学分别
绘制了两幅不完整的统计图（注：每组含最小值，不含最大值）
请你根据图中的信息，解答下列问题：
(1)从图11中可以看出捐款金额在15-20元的人数有多少人？
(2)补全条形统计图，并计算扇形统计图
的值；
(3)全校共有1268人，请你估计全校学生捐款的总金额大约是多少元？
（本题6分）如图，四边形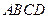
是正方形，点
在
上，
，垂足为
，请你在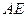
上确定一点
，使
，请你写出两种确定点G的方案，并写出其中一种方案的具体作法和证明．
方案
|
一：
；
|
二：（1）作法：
(2) 证明：（本题5分）先化简
，再选取一个使原式有意义的
的
值代入求值．
如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一
点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动
时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．
（1）当x= ▲s时，DE⊥AB；
（2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；
（3）当△BEF为等腰三角形时，求x的值．