计算: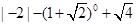
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.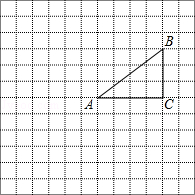
用适当的方法解方程:
(1)x2-2x-1=0(2)3x(x+2)=5(x+2)
某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
| 数量范围(千克) |
0~500 |
500以上~1500 |
1500以上~2500 |
2500以上 |
| 价格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】
(1)如果他批发600千克苹果,则他在A 家批发需要 元,在B家批发需要 元.
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要 元,在B家批发需要 元(用含x的代数式表示).
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理
学校图书馆上周借书记录如下(超过50册的部分记为正,少于50册的部分记为负):
| 星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| 0 |
+8 |
+6 |
-2 |
-7 |
(1)上星期五借出图书多少册?
(2)上星期二比上星期五多借出图书多少册?
(3)上周平均每天借出图书多少册?
阅读下面的材料:
点A、B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,设点A在原点,如图①|AB|=|OB|=|b|=|a-b|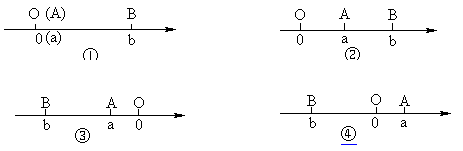
当A、B两点都不在原点时,
如图②,点A,B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|
如图③,点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|
如图④,点A、B在原点的两边, |AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|
综上所述,数轴上A、B两点之间的距离|AB|=|a-b|
请用上面的知识解答下面的问题:
(1)数轴上表示1和5的两点之间的距离是_________,数轴上表示-2和-4的两点之间的距离是__________,数轴上表示1和-3的两点之间的距离是______
(2)数轴上表示x和-1的两点A和B之间的距离是___________,如果|AB|=2,那么x为_______
(3)当|x+1|+|x-2|取最小值时,相应的x的取值范围是______________