如图,过抛物线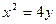 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆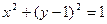 于点A、B、C、D,则
于点A、B、C、D,则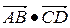 的值是()
的值是()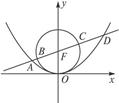
A.8 B.4 C.2 D.1
6个人分乘两辆不同的汽车,每辆车最少坐2人,则不同的乘车方法数为( )
| A.40 | B.50 | C.60 | D.70 |
若函数f(x)的导函数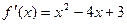 ,则使得函数
,则使得函数 单调递减的一个充分不必要条件是x∈( )
单调递减的一个充分不必要条件是x∈( )
| A.(0,1) | B.[0,2] | C.(2,3) | D.(2,4) |
已知两个等差数列 和
和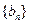 的前
的前 项和分别为A
项和分别为A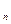 和
和 ,且
,且 ,则使得
,则使得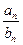 为正偶数时,
为正偶数时, 的值是()
的值是()
| A.1 | B.2 | C.5 | D.3或11 |
知 、
、 、
、 为互不重合的三个平面,命题
为互不重合的三个平面,命题 若
若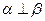 ,
, ,则
,则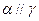 ;命题
;命题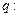 若
若 上不共线的三点到
上不共线的三点到 的距离相等,则
的距离相等,则 。对以上两个命题,下列结论中正确的是()
。对以上两个命题,下列结论中正确的是()
A.命题“ 且 且 ”为真 ”为真 |
B.命题“ 或 或 ”为假 ”为假 |
C.命题“ 或 或 ”为假 ”为假 |
D.命题“ 且 且 ”为假 ”为假 |