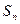为赢得2010年广州亚运会的商机,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值 (单位:万元,
(单位:万元, )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
(本小题满分10分)
(1)计算: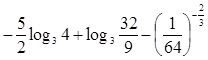
(2)已知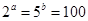 求
求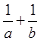 的值
的值
已知全集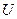 为
为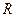 ,集合
,集合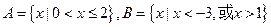
求:(1)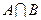 (2)
(2)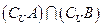 ;(3)
;(3)
(本题10分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上
(Ⅰ)求AB边上的高CE所在直线的方程
(Ⅱ)求△ABC的面积
(本小题满分12分)
已知函数f(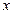 )=
)=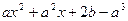 ,当
,当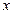 ∈(-2,6)时,其值为正,而当
∈(-2,6)时,其值为正,而当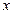 ∈(-∞,-2)∪(6,+∞)时,其值为负
∈(-∞,-2)∪(6,+∞)时,其值为负
(I)求实数 的值及函数f(
的值及函数f(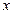 )的解析式
)的解析式
(II)设F(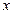 )= -
)= -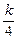 f(
f(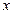 )+4
)+4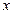 +12
+12 ,问
,问 取何值时,方程F(
取何值时,方程F(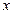 )=0有正根?
)=0有正根?
(本小题满分12分)
已知等比数列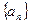 的各项均为正数,且
的各项均为正数,且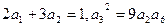
(I)求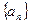 的通项公式
的通项公式
(II)令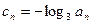 ,求数列
,求数列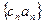 的前n项和
的前n项和