设［x］表示不超过x的最大整数（如［2］="2," ［
］=1）,对于给定的n
N*,定义
，
,则当
时，函数
的值域是( )
A． |
B． |
C． |
D． |
已知函数f（x）＝ax2＋bx＋c （ac≠0），若f（x）＜0的解集为（－1, m），则下列说法正确的是：（）
| A．f（m－1）＜0 | B．f（m－1）＞0 |
| C．f（m－1）必与m同号 | D．f（m－1）必与m异号 |
已知函数y＝
的定义域为A，集合B＝{x||x－3|＜a, a＞0}，若A∩B中的最小元素为2，则实数a的取值范围是：（）
| A．（0, 4] | B．（0, 4） | C．（1, 4] | D．（1, 4） |
定义在R上的函数f（x）满足f（4）＝1．f ′（x）为f（x）的导函数，已知函数y＝f ′（x）的图象如图所示．若两正数a，b满足f（2a＋b）＜1，则的取值范围是（）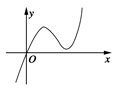
A．（ ， ） |
| B．（－∞，）∪（3，＋∞） |
| C．（，3） |
| D．（－∞，－3） |
对于函数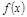
，使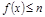
成立的所有常数
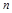中，我们把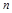的最小值
叫做函数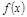的上确界．
则函数
的上确界是（）
| A．0 | B． |
C．1 | D．2 |
下列命题中真命题的个数是（）
①∀x∈R，x4>x2；
②若p∧q是假命题，则p，q都是假命题；
③命题“∀x∈R，x3－x2＋1≤0”的否定是“∃x∈R，x3－x2＋1>0”．
| A．0 | B．1 | C．2 | D．3 |