如图,在梯形ABCD中,AB∥CD,∠BAD=90°,以AD为直径的半圆D与BC相切。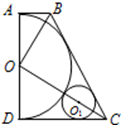
(1)求证:OB⊥OC;
(2)若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积。
如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上,按要求画一个三角形,使它的顶点在方格的顶点上。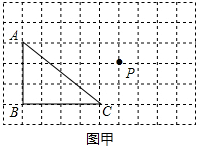
(1)将△ABC平移,使点P落在平移后的三角形内部,在图甲中画出示意图;
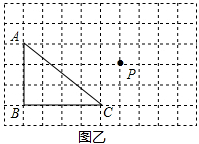
(2)以点C为旋转中心,将△ABC旋转,使点P落在旋转后的三角形内部,在图乙中画出示意图。
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E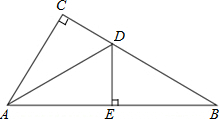
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
化简: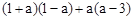
计算: ;
;
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上一动点,连结CD,DE,以CD,DE为边作□CDEF。
(1)当0< m <8时,求CE的长(用含m的代数式表示);
(2)当m =3时,是否存在点D,使□CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得□CDEF为矩形,请求出所有满足条件的m的值。