水平轨道PQ、MN两端各接一个阻值R1=R2=8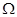 的电阻,轨道间距L=1.0m,轨道很长,轨道电阻不计。轨道间磁场按如图所示的规律分布,其中每段垂直纸面向里和向外的磁场区域宽度均为10cm,磁感应强度大小均为B=1.0T,每段无磁场的区域宽度均为20cm,导体棒ab本身电阻r=1.0
的电阻,轨道间距L=1.0m,轨道很长,轨道电阻不计。轨道间磁场按如图所示的规律分布,其中每段垂直纸面向里和向外的磁场区域宽度均为10cm,磁感应强度大小均为B=1.0T,每段无磁场的区域宽度均为20cm,导体棒ab本身电阻r=1.0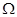 ,导体棒与导轨接触良好。现使导体棒ab以
,导体棒与导轨接触良好。现使导体棒ab以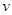 =1.0m/s的速度始终向右匀速运动。求:
=1.0m/s的速度始终向右匀速运动。求:
(1)当导体棒ab从左端进入磁场区域开始计时,设导体棒中电流方向从b流向a为正方向,通过计算后请画出电流随时间变化的i-t图像;
(2)整个过程中流过导体棒ab的电流为交变电流,求出流过导体棒ab的电流有效值。(结果保留2位有效数字)
总质量为100 kg的小车,在粗糙水平地面上从静止开始运动,其速度—时间图象如图所示。已知在0—2s时间内小车受到恒定水平拉力F = 1240N,2s后小车受到的拉力发生了变化。试根据图象求:(g取10 m/s2)
(1)0 — 18时间内小车行驶的平均速度约为多少?
(2)t ="1" s时小车的加速度 ;
;
(3)小车与地面间的动摩擦因数 。
。
)(如图所示,质量为 的小物块以水平速度
的小物块以水平速度 滑上原来静止在光滑水平面上质量为
滑上原来静止在光滑水平面上质量为 的小车上,物块与小车间的动摩擦因数为
的小车上,物块与小车间的动摩擦因数为 ,小车足够长。求:
,小车足够长。求:
①小物块相对小车静止时的速度;
②从小物块滑上小车到相对小车静止所经历的时间;
③从小物块滑上小车到相对小车静止时,系统产生的热量和物块相对小车滑行的距离。
如图所示,一束截面为圆形(半径R=1 m)的平行紫光垂直射向一半径也为R的玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区.屏幕S至球心的距离为D=(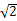 +1) m,不考虑光的干涉和衍射,试问:
+1) m,不考虑光的干涉和衍射,试问: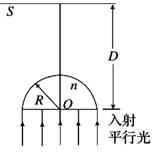
①若玻璃半球对紫色光的折射率为n=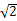 ,请你求出圆形亮区的半径.
,请你求出圆形亮区的半径.
②若将题干中紫光改为白光,在屏幕S上形成的圆形亮区的边缘是什么颜色?
如图所示,水平传送带的右端与竖直面内的用光滑钢管弯成的“9”形固定轨道相接,钢管内径很小。传送带的运行速度为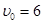 m/s,将质量
m/s,将质量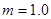 kg的可看作质点的滑块无初速地放到传送带
kg的可看作质点的滑块无初速地放到传送带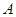 端,传送带长度为
端,传送带长度为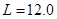 m,“9”字全高
m,“9”字全高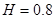 m,“9”字上半部分圆弧半径为
m,“9”字上半部分圆弧半径为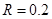 m,滑块与传送带间的动摩擦因数为
m,滑块与传送带间的动摩擦因数为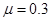 ,重力加速g=10m/s2,试求:
,重力加速g=10m/s2,试求: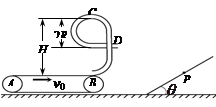
(1)滑块从传送带A端运动到B端所需要的时间;
(2)滑块滑到轨道最高点C时对轨道作用力的大小和方向;
(3)若滑块从“9”形轨道D点水平抛出后,恰好垂直撞在倾角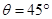 的斜面上P点,求P、D两点间的竖直高度 h(保留两位有效数字)。
的斜面上P点,求P、D两点间的竖直高度 h(保留两位有效数字)。
在一次低空跳伞训练中,当直升机悬停在离地面224m高处时,伞兵离开飞机做自由落体运动。运动一段时间后,打开降落伞,展伞后伞兵以12.5m/s2的加速度匀减速下降。为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s,求:(取g=10m/s2)

(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下?
(2)伞兵在空中的最短时间为多少?