定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系.在平面斜坐标系 中,若
中,若 (其中
(其中 分别是斜坐标系中的
分别是斜坐标系中的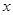 轴和
轴和 轴正方向上的单位向量,
轴正方向上的单位向量,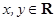 ,
, 为坐标原点),则称有序数对
为坐标原点),则称有序数对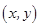 为点
为点 的斜坐标.在平面斜坐标系
的斜坐标.在平面斜坐标系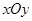 中,若点
中,若点 的斜坐标为(1,2),点
的斜坐标为(1,2),点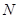 的斜坐标为(3,4),且
的斜坐标为(3,4),且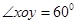 ,则
,则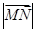 等于 ( )
等于 ( )
| A.1 | B.2 | C. |
D.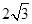 |
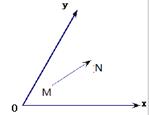
若条件 的()
的()
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知集合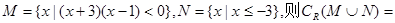 ()
()
A.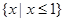 |
B.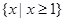 |
C.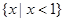 |
D.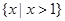 |
已知a>0且a≠1,若函数f(x)= loga(ax2 –x)在[3,4]是增函数,
则a的取值范围是( )
| A.(1,+∞) | B.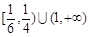 |
C.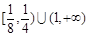 |
D.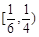 |
若函数f(x)=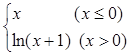 ,若f(2-x2)>f(x),则实数x的取值范围是( )
,若f(2-x2)>f(x),则实数x的取值范围是( )
| A.(-∞,-1)∪(2,+∞) | B.(-2,1) |
| C.(-∞,-2)∪(1,+∞) | D.(-1,2) |
对于函数f(x)定义域中任意的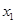 ,
,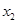 (
(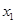 ≠
≠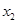 ),有如下结论:
),有如下结论:
①f(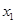 +
+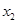 )=f(
)=f(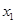 )·f(
)·f(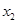 )
)
②f(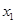 ·
·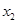 )=f(
)=f(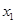 )+f(
)+f(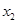 )
)
③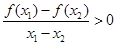
④
当f(x)=lgx时,上述结论中正确结论的序号是()
| A.①② | B.②③ | C.③④ | D.②③④ |