已知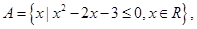

(1)若 ,求实数
,求实数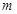 的值;
的值;
(2)若
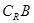 ,求实数
,求实数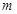 的取值范围.
的取值范围.
已知函数f(x)是定义域在R上的奇函数,当x>0时,f(x)=x2﹣2x.
(1)求出函数f(x)在R上的解析式;
(2)写出函数的单调区间.
已知集合M={x|x2﹣3x≤10},N={x|a+1≤x≤2a+1}.
(1)若a=2,求M∩(∁RN);
(2)若M∪N=M,求实数a的取值范围.
(1)若xlog32=1,试求4x+4﹣x的值;
(2)计算:(2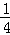 )
) ﹣(﹣9.6)0﹣(3
﹣(﹣9.6)0﹣(3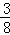 )
)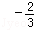 +(1.5)﹣2+(
+(1.5)﹣2+(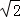 ×
×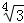 )4.
)4.
已知函数f(x)=x3+x.
(1)判断函数f(x)的单调性与奇偶性,(不用证明结论).
(2)若f(cosθ﹣m)+f(msinθ﹣2)<0对θ∈R恒成立,求实数m的取值范围.
已知向量 =(cosα,sinα),
=(cosα,sinα),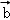 =(cosβ,sinβ),|
=(cosβ,sinβ),| ﹣
﹣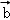 |=
|= .
.
(1)求cos(α﹣β)的值;
(2)若0<α<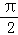 ,﹣
,﹣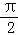 <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ,求sinα.
,求sinα.