1962年11月,美国马里兰州上空的一架飞机——“子爵号”正平稳地飞行,突然一声巨响,飞机坠落,飞机上的人全部遇难.原来飞机和一只翱翔的天鹅相撞,天鹅变成了“炮弹”,击毁了赫赫有名的“子爵号”.
1980年秋,前苏联一架客机从矿水城起飞,五分钟之后突然遭到“袭击”,驾驶舱玻璃和降落灯被击得粉碎,领航员身负重伤.经调查,这次事故的原因是客机和一群野鹅相撞.见图.
浑身是肉的鹅,为什么能击毁坚硬的飞机呢?请你简要回答.
在如图所示的电路中,R1、R2均为定值电阻,且R1=100Ω,R2阻值未知,R3是一滑动变阻器,当其滑片从左端滑至右端时,测得电源的路端电压随电流的变化图线如图所示,其中A、B两点是滑片在变阻器的两个不同端点得到的求: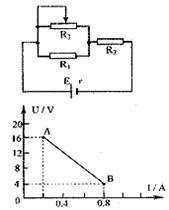
(1)电源的电动势和内阻;
(2)定值电阻R2的阻值;
(3)滑动变阻器的最大阻值。
如图所示,两根相距L平行放置的光滑导电轨道,与水平面的夹角均为  ,轨道间有电阻R,处于磁感应强度为B、方向竖直向上的匀强磁场中,一根质量为m、电阻为r的金属杆ab,由静止开始沿导电轨道下滑.设下滑中ab杆始终与轨道保持垂直,且接触良好,导电轨道有足够的长度,且电阻不计.求:
,轨道间有电阻R,处于磁感应强度为B、方向竖直向上的匀强磁场中,一根质量为m、电阻为r的金属杆ab,由静止开始沿导电轨道下滑.设下滑中ab杆始终与轨道保持垂直,且接触良好,导电轨道有足够的长度,且电阻不计.求:
(1)ab杆将做什么运动 ?若开始时就给ab沿轨道向下的拉力F使其由静止开始向下做加速度为a的匀加速运动 ( ).求拉力F与时间t的关系式.
).求拉力F与时间t的关系式.
如图,直线MN 上方有平行于纸面且与MN成45。的有界匀强电场,电场强度 大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点出发记为第一次经过直线MN,而第五次经过直线MN时恰好又通过O点。不计粒子的重力。求:
大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点出发记为第一次经过直线MN,而第五次经过直线MN时恰好又通过O点。不计粒子的重力。求:
(1)电场强度的大小;
(2)该粒子再次从O点进入磁场后,运动轨道的半径;
(3)该粒子从O点出发到再次回到O点所需的时间。
一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω,金属框放在表面绝缘且光滑的斜面顶端(金属框上边与AA′重合),自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合),设金属框在下滑过程中的速度为v,与此对应的位移为s,那么v2—s图象如图所示,已知匀强磁场方向垂直斜面向上,g=10m/s2。
(1)根据v2—s图象所提供的信息,计算出斜面倾角θ和匀强磁场宽度d.
(2)金属框从进入磁场到穿出磁场所用的时间是多少?
(3)匀强磁场的磁感应强度多大?
如图所示的木板由倾斜部分和水平部分组成,两部分之间由一段圆弧面相连接。在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m 、半径均为r的均匀刚性球,在施加于1号球的水平外力F的作用下均静止,力F与圆槽在同一竖直面内,此时1号球球心距它在水平槽运动时的球心高度差为h.现撤去力F使小球开始运动,直到所有小球均运动到水平槽内.重力加速度为g。求:
⑴水平外力F的大小;
⑵1号球刚运动到水平槽时的速度大小;
⑶整个运动过程中,2号球对1号球所做的功。