已知函数f(x)＝
x3＋
x2－ax－a，x∈R，其中a＞0.
（1）求函数f(x)的单调区间；
（2）若函数f(x)在区间(－2,0)内恰有两个零点，求a的取值范围；
（3）当a＝1时，设函数f(x)在区间[t，t＋3]上的最大值为M(t)，最小值为m(t)，记g(t)＝M(t)－m(t)，求函数g(t)在区间[－3，－1]上的最小值.
（本小题满分12分）已知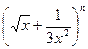
的第五项的二项式系数与第三项的二项式系数的比是14:3，求展开式中的常数项.
函数f(x)＝x3＋3ax2＋3bx＋c在x＝2处有极值，其图象在x＝1处的切线平行于直线3x＋y＋2＝0．
（1）求a，b的值； （2）求函数的极大值与极小值的差．
已知函数
的最小正周期为
（1）求
的值；（2）求函数f(x)的单调递增区间；
（3）求函数f(x)在区间[0，
]上的取值范围．
已知向量
，
=（1，2）．
（１）若
，求tan
的值； （２）若
，
，求的值．
海上有A，B两个小岛相距10n mile，从A岛望B岛和C岛所成的视角为60°，从B岛望A岛和C岛所成的视角为75°．试求B岛和C岛间的距离．