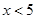“十一”黄金周期间,井冈山红色旅游在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 人数变化 单位:万人 |
+1.2 |
+0.8 |
+0.6 |
-0.4 |
-0.6 |
+0.2 |
-1.2 |
(1)、若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客_________万人。
(2)、请判断七天内游客人数最多的是_______日;最少的是______日。它们相差___________万人?
(3)、以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数情况:
人数变化(万人)
如果方程组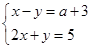 的解x、y满足x>0.y<0求a的取值范围.
的解x、y满足x>0.y<0求a的取值范围.
.解不等式组.并把解集在数轴上表示出来. (1)
(1)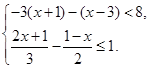 (2)
(2) 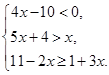
(3)-7≤ ≤9.
≤9. (4)
(4)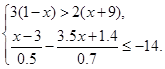
在“5 12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000
12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 和乙种板材12000
和乙种板材12000 的任务(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30
的任务(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30 或乙种板材20
或乙种板材20 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间 型板房和一间
型板房和一间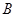 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
 型板房 型板房 |
54  |
26  |
5 |
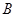 型板房 型板房 |
78  |
41  |
8 |
问:这400间板房最多能安置多少灾民?
(本小题7分)关于 ,
,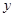 的方程组
的方程组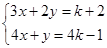 的解
的解 ,
,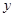 满足
满足 ,求
,求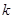 的取值范围.
的取值范围.
(本小题5分)分别在数轴上画出下列解集.
⑴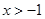 ;⑵
;⑵ ;⑶
;⑶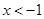 ;⑷
;⑷ ;⑸
;⑸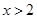 且
且