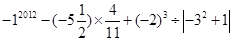图1是一个长为2
，宽为2
的长方形，沿图中虚线剪开，可分成四块小长方形.
（1）求出图1的长方形面积；
（2）将四块小长方形拼成一个图2的正方形．利用阴影部分面积的不同表示方法，直接写出代数式（
）2、（
）2、
之间的等量关系；
（3）把四块小长方形不重叠地放在一个长方形的内部（如图3），未被覆盖的部分用
阴影表示．求两块阴影部分的周长和（用含
、
的代数式表示）.
如图，四边形OABE中，∠AOE=∠BEO=90°，OA=3， OE==4，BE=1，点C，D是边OE（与端点O、E不重合）上的两个动点且CD=1．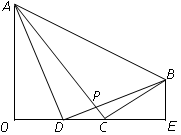
（1）求边AB的长；
（2）当△AOD与△BCE相似时，求OD的长.
（3）连结AC与BD相交于点P，设OD=x，△PDC的面积记为y，求y关于x的函数关系式，并写出x的取值范围．
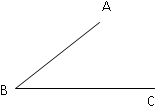
如图，如果直线L上依次有3个点A、B、C，那么
（1）在直线L上共有多少射线？多少条线段？
（2）在直线L上增加一个点，共增加了多少条射线？多少条线段？
（3）如果在直线L上增加到n个点，则共有多少条射线？多少条线段？
如图，网格中每一个小正方形的边长为1个单位长度．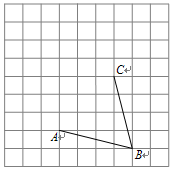
（1）请在所给的网格内画出以线段AB、BC为边的菱形ABCD；
（2）填空：菱形ABCD的面积等于________________．
如图，已知∠ABC．请你再画一个∠DEF，使DE∥AB，EF∥BC，且DE交BC边与点P．探究：∠ABC 与 ∠DEF 有怎样的数量关系？并说明理由（需要证明）．
